Почему?
Я буду обсуждать этот вопрос с точки зрения интерполяции некой известной кривой (например, хотим подменить спираль Корню сплайном, чтобы не мучаться с интегралами Френеля).
1. Начнём с того, что разные наборы

дают разные сплайны. И, стало быть, вопрос просто достоин обдумывания.
2. Рекомендацию использовать накопленную длину хорды (вот! по этому ключевому слову я и сыщу, наверное, --- что я когда-то писал на эту тему на форуме) я где-то очень давно вычитал. Для себя придумал следующее обоснование. Всё же мы при построении сплайна приравниваем производные по тэ в узлах интерполяции. И такой подход делает это приравние более осмысленным. Да, такой выбор параметра делает его близким к натуральному.
3. Для себя придумал ещё одну фулечку. Строго говоря, мы должны ещё откуда-то взять граничные условия на производные. Всякие трюки типа понижения порядка сплайна на концах и др. заточены на то, чтобы не думать о граничных условиях, что иногда уместно. Но в примере с той же спиралью Корню мне известны наклоны касательных на концах,

и
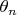
, и грех их не использовать для повышения точности интерполяции. Если я считаю параметр близким к натуральному, то кусочные полиномы кубического сплайна можно считать близкими к разложению
![$[x(t),y(t)]$ $[x(t),y(t)]$](https://dxdy-01.korotkov.co.uk/f/8/f/f/8ff6b68a143abfbc1d45f82f325dcd8382.png)
в ряд Тейлора, а в качестве производных на концах тогда осмыслены

.
4. Все эти соображения уместны только в том случае, если икс и игрек одинакового (геометрического) происхождения. Если этот эллипс произошёл от какого-то "фазового портрета" (забыл, что это такое), и указывает допустимую связь тока и напряжения, или метров и секунд, то выписанная выше длина хорды бессмысленна. Но тогда в задаче скорее всего существует какой-то коэффициент, параметр, позволяющий осмыслить и это.
Судя по всему, процесс должен быть сходящимся.
5. Да, дело очень быстро сходится, но уточнения при итерациях мизерны (это я вспоминаю результаты своих давних опытов).
-- 20 июн 2013, 16:14:28 --Нашёл:
Я уже пел эту арию в сообщении #164828.