Восстановление векторных сомножителей

[serval]

serval в сообщении #737925 писал(а):

В трехмерном случае, по крайней мере, можно.

А как? Можете показать?

P.S. Смысл, конечно, есть и я поясню его как только будет решена поставленная задача.

[svv]

Я загадываю $m$ и $n$ и нахожу векторное произведение $[p_m, p_n]=c$.
Так как $p_n=\left(1, n, \frac {(n-1)n}2\right)$, то компоненты $c=(x, y, z)$ равны

$$\begin{cases}x=\dfrac{mn(n-m)}2\\[2ex]y=\dfrac{m^2-n^2+n-m}2\\[1.2ex]z=n-m\end{cases}$$

Я их Вам сообщаю, а Вы должны угадать $m$ и $n$. Попробуйте решить.
Здесь избыточная информация, т.е. можно проверять корректность входных данных.

[Otta]

Ой, ну лениво же ж писать. :)

Вы бы лучше смысл, а там, глядишь, и задачу в общем случае решать легче.

Я просто в лоб посмотрела. Выписываем вектор $(1, k, k(k-1)/2)$ и вектор $(1, l, l(l-1)/2)$. Считаем векторное произведение $p=(l-k)(kl/2, -(l+k-1)/2,1)$. Поэтому векторное произведение равно нулю только в том случае, когда $l=k$. Уже хорошо.

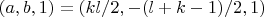
Дальше. Пусть известно, что $p$ - произведение "специальных" векторов. Надо понять, единственным ли образом они определяются. Случай нулевого вектора разобран, смотрим, когда он ненулевой. Тогда $l\ne k$. И вектор, коллинеарный $p$, $(a,b,1)=(kl/2, -(l+k-1)/2,1)$. Соответствующая система решается однозначно.

[serval]

Я весь день думал в другую сторону, сейчас пялюсь на простую вещь и понимаю, что жутко торможу.
Пожалуйста, просто напишите решение. Объяснение смысла обещаю не позже завтрашнего дня (мог бы сейчас, но уезжаю из города и не знаю как обернусь).

P.S. Кстати, как вычислять элементы следующих столбцов треугольника Паскаля догадаться несложно. Можете попробовать решить задачу для бОльших размерностей, а смысл я Вам обещаю :)

[Otta]

serval в сообщении #737942 писал(а):

Я весь день думал в другую сторону, сейчас пялюсь на простую вещь и понимаю, что жутко торможу.
Пожалуйста, просто напишите решение.

Ну Вы садист.
Просто решение просто: взять два ваших вектора, перемножить, посмотреть, что получится, обозначить, что получилось, новыми переменными, попытаться выразить старые переменные через новые. И все.

[serval]

Вот на это и пялюсь. Кстати, одну вторую тоже можно вынести.

[Otta]

serval в сообщении #737942 писал(а):

Кстати, как вычислять элементы следующих столбцов треугольника Паскаля догадаться несложно.

Если вместо "столбцов" должно стоять "строк", то нас с svv этому давно научили. Спасибо, конечно, но Вы лучше ближе к теме.

[serval]

Когда добавится 4-я координата для нее потребуется формула зависящая от номера строки. Но все элементы 4-го столбца будут вычисляться по одной формуле. И всех последующих тоже.
Или это я снова торможу? Пора домой :)

[Otta]

serval в сообщении #737950 писал(а):

Но все элементы 4-го столбца будут вычисляться по одной формуле. И всех последующих тоже.

Угу. Не все. Но те, которые ненулевые, будут равны $C^3_n$. И всех последующих нетрудно догадаться чему.

[Xaositect]

Все гораздо проще, если вспомнить геометрическое описание в.п. Никакие три вектора из рассматриваемых не лежат в одной плоскости (очевидно из выпуклости $\frac{x(x+1)}{2}$), значит, если нам дали векторное произведение, надо провести нормальную к нему плоскость, найти или не найти на ней два вектора и проверить, подходят ли они.

[serval]

Xaositect в сообщении #737953 писал(а):

те, которые ненулевые

В треугольнике Паскаля все ненулевые. И все элементы столбца $C^3_n$ вычисляются по одной - не рекуррентной - формуле зависящей только от номера строки.

Xaositect в сообщении #737953 писал(а):

если вспомнить геометрическое описание

Геометрически это значит, что вектор заданный тремя первыми элементами строки треугольника Паскаля заметает поверхность которая в трехмерии сечется одной плоскостью ровно дважды.

[Otta]

serval в сообщении #738021 писал(а):

В треугольнике Паскаля все ненулевые.

Вы не все строки берете из строк треугольника с номером, не меньшим трех. Во всяком случае, это не оговаривалось.

serval в сообщении #738021 писал(а):

И все элементы столбца вычисляются по одной - не рекуррентной - формуле зависящей только от номера строки.

Тут я не поняла. Мы друг друга убеждаем в одном и том же?

[serval]

Otta в сообщении #738022 писал(а):

Вы не все строки берете из строк треугольника

Все. Строки с нулевыми компонентами работают одинаково с другими.

Otta в сообщении #738022 писал(а):

Мы друг друга убеждаем в одном и том же?

А вы напишите формулу для 4-го столбца и станет ясно :)

[svv]

serval писал(а):

И все элементы столбца $C^3_n$ вычисляются по одной - не рекуррентной - формуле зависящей только от номера строки.

serval писал(а):

А вы напишите формулу для 4-го столбца и станет ясно :)

Значок $C^3_n$, который Otta написала, это не обозначение этих элементов, это готовая, законченная формула для их значений.
См. статью в Википедии.

[Otta]

svv, спасиб. А то я уже не знала, на какой язык мне переходить.
Но возможно, дело в том, что serval вычислил $C^3_k=k(k-1)(k-2)/6$ явно, а полученное выражение у него с числом сочетаний не ассоциируется. Это раз.
Два. При $k<3$ элементом столбца будет все же не число сочетаний, а 0.