Цитата:
А что это за вид? Обычно же вид такой:

.
Этот вид предложил преподаватель, впоследствии такой же я обнаружил в учебнике "Введение в дискретную математику" Яблонского.
Так, я домыслю:

,

- состояния МТ,

- шаги.
А вот тут можно поподробнее? Не очень понятно, как это конкретно делается. Вообще не понятно, как на этом языке реализовать условие. Предполагаю

А из
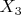
никуда не уходим? Или
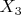
- конечное состояние? (обычно пишут

).
Воспроизвел работу программы, это больше похоже на вычисление

(здесь

- усеченная разность).
Вам надо такую рекурсию воспроизвести: если на входе

или

, то

следует интепретировать как четность входа, а

- как нечетность (если задана другая схема кодирования выхода - перекодировать после вычисления). А если на входе

, то нужно вычислить

- просто стереть две единички. (можно проще описать, но полностью решать за Вас не могу).
Еще играют роль технические вещи: у Вас лента потенциально неограниченна в одну сторону или в две? Если в одну, то как определить начало левого края входа? Если он слева ноликом не обрамлен - придется это сначала сделать.
Попытайтесь, это несложно.
A вот умножать- что- то совсем глухо. Не могли бы вы поподробнее объяснить?
Рекурсия такая:


,
т.е. пока

ненулевое, выполнять сложение (сначала нужно написать МТ для сложения, а затем ее юзать как подпрограмму в искомой МТ). Вы МТ для сложения можете написать?