Вот я вчера лопухнулся: в обратную сторону у меня не получается строго доказать: если
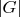
четно, то не всякий элемент - квадрат. Нутром чувствую, что так, а доказать не могу

(Оффтоп)
Наша команда просто пьяна, вероятно в этом

. Но всеже, спассибо.
Как-то раз решал что-то олимпиадное с похмелья. На удивление решалось хорошо и притом интуитивно, в виде инсайтов

Ааа! До меня дошло! Пусть
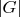
четное.

разбивается на пары взаимно обратных элементов. Но

! Значит есть еще один

