Есть пара вопросов по доказательствам к следствияем из теоремы. Сначала быстро приведу их содержание (из книги Колмогорова):
Теорема (Банаха об обратном операторе). Пусть

- линейный ограниченный оператор, взаимнооднозначно отображающий банахово пространство (БП)

на БП

. Тогда обратный оператор ограничен.
Следствие 1. (т. об открытом отображении). Линейное непрерывное отображение

БП

на (всё) БП

открыто.
Это вытекает из теоремы и следующей леммы:
Пусть

- БП и

- некоторое его замкнутое подпространство. Отображение

протранства

на фактор-пространство

, ставящее в соответствие каждому

из

класс смежности, содержащий

, открыто.
Доказательство следствия. Представив отображение

пространства

на

как суперпозицию отображения

пространства

на

(открытого в силу леммы) и взаимно однозначного отображения

пространства

на

(
открытого в силу теоремы), получаем, что

открыто.
Первый вопрос, почему отображение

открыто, как это следует из теоремы?
Следствие 2. (лемма о тройке). Пусть
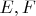
и

- БП и

- непрерывные линейные операторы из

в

и из

в

, причем

отображает

на все

. Если при этом
 (1)
(1), то существует такой непрерывный линейный оператор

, отображающий

в

, что

.
Доказательство. Рассмотрим для каждого элемента

из

его полный прообраз

. Из условия
(1) следует, что все элементы x, принадлежащие

, переводятся оператором

в один и тот же элемент

...
Второй вопрос, непонятно, как это следует из условия?
Буду рад, если кто подскажет.