О касательных к кривой Ферма

[Vladislav Evg K]

Материал, который будет размещен ниже, состоит из четырех небольших частей, и подготовлен для публикации в журнальном виде.
По некоторым причинам я принял решение разместить его здесь, поэтому прошу понимания в том, что хотя стиль изложения и обороты речи в нем могут не соответствовать общепринятым правилам конференции, все же не требовать от меня невозможного и разрешить оставить «все как есть».

Ввиду того, что TEX я пользуюсь в первый раз, заранее прошу извинить меня за возможные ошибки, хотя постараюсь их не допускать.

-- 13.01.2013, 22:36 --

Первая часть

Сделаем попытку доказательства Великой теоремы Ферма. Мы покажем это на самом простом примере, который однако не поддавался до сих пор элементарному доказательству.

$$x^3 + y^3 = 1 \eqno (1)$$

Графически это уравнение выглядит следующим образом:

Предположим, что на кубике имеется рациональная точка А с координатами $\left[ {x_0 ;y_0 } \right]$

$$x_0^3 + y_0^3 = 1 \eqno (2)$$

Если в дальнейшем при каких-либо непротиворечивых рассуждениях мы все-таки придем к противоречию, то вынуждены будем снять свое предположение о наличии рациональной точки А на кубике.
Начнем рассуждения с простого – проведем касательную к кубике в точке А. Касательная к кривой $y = f\left( x \right)$ в точке $\left[ {x_0 ;y_0 } \right]$ определяется уравнением:

$$y - f\left( {x_0 } \right) = f\prime \left( {x_0 } \right)\left( {x - x_0 } \right) \eqno (3)$$

Находим вначале промежуточные значения:

$$f\left( {x_0 } \right) = y_0 $$

$$f\left( x \right) = \sqrt[3]{{1 - x^3 }} = \left( {1 - x^3 } \right)^{\frac{1} {3}}$$

$$f\prime \left( x \right) = \frac{1} {2}\left( {\frac{{1 - x_0 x^2 }} {{y_0 }}} \right)^{ - \frac{1} {2}} \left( {\frac{{1 - x_0 x^2 }} {{y_0 }}} \right)^\prime = \frac{1} {2}\frac{{y_0^{\frac{1} {2}} \left( { - 2x_0 x} \right)}} {{y_0 \left( {1 - x_0 x^2 } \right)^{\frac{1} {2}} }} = - \frac{{x_0 x}} {{y_0^{\frac{1} {2}} \left( {1 - x_0 x^2 } \right)^{\frac{1} {2}} }}$$

$$f\prime \left( {x_0 } \right) = - \frac{{x_0^2 }} {{y_0^2 }}$$

И подставляем их в (3):

$$y - y_0 = - \frac{{x_0^2 }} {{y_0^2 }}\left( {x - x_0 } \right)$$

$$y = - \frac{{x_0^2 }} {{y_0^2 }}x + \frac{{x_0^2 }} {{y_0^2 }}x_0 + y_0 = - \frac{{x_0^2 }} {{y_0^2 }}x + \frac{{x_0^3 + y_0^3 }} {{y_0^2 }} = - \frac{{x_0^2 }} {{y_0^2 }}x + \frac{1} {{y_0^2 }}$$

Итак, уравнение касательной к кубике в точке $A\left[ {x_0 ;y_0 } \right]$

$$y = - \frac{{x_0^2 }} {{y_0^2 }}x + \frac{1} {{y_0^2 }}\eqno (4)$$

Предполагая определенность значений $x_0$ и $y_0$ , можно сделать вывод о единственности касательной к кубике в точке А.
Во второй части мы проведем еще одну касательную к той же кубике в той же рациональной точке А, которая однако не будет совпадать с уже проведенной касательной.
Такое невозможно представить, если действовать обычным образом (именно так мы только что действовали).
Образно говоря, мы подойдем к этому не через парадные ворота устоявшегося метода, а через малозаметный боковой проезд.
И сумма этих двух подходов покажет нам Дворец Истины не в виде обычной плоской картинки, а виде 3D модели «поистине удивительного» вида.

[Vladislav Evg K]

Вторая часть

Сейчас мы займемся чем-то вроде проверки IQ.
Например, решением задач типа: «Найдите закономерность и продолжите ряд».

Пусть дана такая последовательность (символы английского алфавита):
b, a, e, o, s, q, t, d, u, n…
Нужно продолжить ряд.
Это трудная задача и мы ею заниматься не будем.

Наша задача будет проще, в чем вы сможете сейчас убедиться.
Для начала преобразуем уравнение касательной (4) таким образом:

$$ y = - \frac{{x_0^2 }} {{y_0^2 }}x + \frac{1} {{y_0^2 }} $$

$$ y_0^2 y = - x_0^2 x + 1 $$

$$x_0^2 x + y_0^2 y = 1 \eqno (5)$$

Именно такой вид уравнения касательной будет для нас наиболее полезен.

Теперь мы имеем:
1. уравнение ВТФ для $n = 3$

$$x^3 + y^3 = 1$$

2. уравнение касательной (5)

$$x_0^2 x + y_0^2 y = 1$$

3. и, наконец, само предполагаемое решение уравнения

$$x_0^3 + y_0^3 = 1$$

Представим их совместно, в виде системы уравнений:

$$ \left\{ \begin{gathered} x^3 + y^3 = 1 \hfill \\ x_0^2 x + y_0^2 y = 1 \hfill \\ x_0^3 + y_0^3 = 1 \hfill \\ \end{gathered} \right \eqno (6)$$

Посмотрите внимательно на эту систему – она этого заслуживает.
Посмотрели?
Тогда я предложу вам задачу, сформулировав ее таким образом: «Найдите закономерность и вставьте пропущенный член».
Проверьте себя!

Надеюсь, что вы уже нашли его. Вот он:

$$x_0 x^2 + y_0 y^2 = 1\eqno (7)$$

Итак, имеем:

$$\left\{ \begin{gathered} x^3 + y^3 = 1 \hfill \\ x_0 x^2 + y_0 y^2 = 1 \hfill \\ x_0^2 x + y_0^2 y = 1 \hfill \\ x_0^3 + y_0^3 = 1 \hfill \\ \end{gathered} \right\eqno (8)$$

Не правда ли, весьма стройная система получилась.
Что же в ней означает новое уравнение (7)?
Значения переменных здесь второй степени, следовательно – это кривая второго порядка. А если вспомнить классическое уравнение эллипса:

$$\frac{{x^2 }} {{a^2 }} + \frac{{y^2 }} {{b^2 }} = 1$$

где a, b – оси эллипса, то придется признать, что новое уравнение в системе описывает эллипс.

Причем, на нем обязана присутствовать и наша точка A. И вообще, точка A входит во все уравнения системы (8). Входит в виде решения этой системы уравнений.

Т.е. мы предположили в начале единственное – пусть рациональная точка $A\left[ {x_0 ;y_0 } \right]$ лежит на кубике:

$$\left\{ \begin{gathered} x^3 + y^3 = 1 \hfill \\ x_0^3 + y_0^3 = 1 \hfill \\ \end{gathered} \right$$

а получили целую систему уравнений (8), каждое из которых также содержит эту рациональную точку.

Из этой системы уравнений нас интересует естественно эллипс, ибо касательная проста как простая прямая, а кубика сложна до невозможности.

Докажем, что этот эллипс является касательным к кубике в точке A. Для этого к кривой эллипса

$$x_0 x^2 + y_0 y^2 = 1$$

проведем касательную в точке $A\left[ {x_0 ;y_0 } \right]$.
Чтобы это сделать, повторим действия, описанные в Первой части.

$$y - f\left( {x_0 } \right) = f\prime \left( {x_0 } \right)\left( {x - x_0 } \right) \eqno (3)$$

Находим вначале промежуточные значения:

$$f\left( {x_0 } \right) = y_0$$

$$f\left( x \right) = \sqrt {\frac{{1 - x_0 x^2 }} {{y_0 }}} = \left( {\frac{{1 - x_0 x^2 }} {{y_0 }}} \right)^{\frac{1} {2}} $$

$$f\prime \left( x \right) = \frac{1} {2}\left( {\frac{{1 - x_0 x^2 }} {{y_0 }}} \right)^{ - \frac{1} {2}} \left( {\frac{{1 - x_0 x^2 }} {{y_0 }}} \right)^\prime = \frac{1} {2}\frac{{y_0^{\frac{1} {2}} \left( { - 2x_0 x} \right)}} {{y_0 \left( {1 - x_0 x^2 } \right)^{\frac{1} {2}} }} = - \frac{{x_0 x}} {{y_0^{\frac{1} {2}} \left( {1 - x_0 x^2 } \right)^{\frac{1} {2}} }}$$

$$ f\prime \left( {x_0 } \right) = - \frac{{x_0 x_0 }} {{y_0^{\frac{1} {2}} \left( {1 - x_0 x_0^2 } \right)^{\frac{1} {2}} }} = - \frac{{x_0^2 }} {{y_0^{\frac{1} {2}} \left( {y_0^3 } \right)^{\frac{1} {2}} }} = - \frac{{x_0^2 }} {{y_0^2 }} $$

Подставляем их в (3):

$$ y - y_0 = - \frac{{x_0^2 }} {{y_0^2 }}\left( {x - x_0 } \right) $$

$$ y = - \frac{{x_0^2 }} {{y_0^2 }}x + \frac{{x_0^2 }} {{y_0^2 }}x_0 + y_0 = - \frac{{x_0^2 }} {{y_0^2 }}x + \frac{{x_0^3 + y_0^3 }} {{y_0^2 }} = - \frac{{x_0^2 }} {{y_0^2 }}x + \frac{1} {{y_0^2 }} $$

Следовательно, касательная к эллипсу имеет вид:

$$ y = - \frac{{x_0^2 }} {{y_0^2 }}x + \frac{1} {{y_0^2 }} $$

Таким образом получили, что и к кубике

$$ x^3 + y^3 = 1 $$

и к эллипсу

$$ x_0 x^2 + y_0 y^2 = 1 $$

касательной (в точке их касания A) служит одна и та же прямая:

$$ x_0^2 x + y_0^2 y = 1 $$

Следовательно, эллипс является касательным к кубике в точке A.

Аналогом этого, для наглядности, может быть следующее утверждение: если a = c и b = с, то a = b

Вот мы и провели вторую касательную к кубике в точке A, не совпадающую с первой касательной.

Позволю себе немного пояснений.
Новая касательная образована из исходной кривой (кубики) точно по такому же наглядному алгоритму, как и обычная касательная (см. систему уравнений (8)) и, как только что мы доказали, является касательной к кубике.
Другой вопрос – существует бесконечное множество эллипсов другого размера и формы, также касательных к кубике в точке A. Возможно, в этом и кроется причина не введения в математику до сих пор подобных объектов. Однако это не является для нас причиной отказа от тех возможностей, которые предоставляют нам такие объекты. Особенно появившихся вышеописанным способом, который открылся нам как Дар Небес (и за который мы должны благодарить кого-то из тех, кто стоит выше нас).
Из этого множества мы выбрали вариант, который наиболее прост и логичен по своему образованию, который, также как и простая касательная, единственен для конкретной точки касания на исходной кривой, и мы намерены использовать его потенциал, по крайней мере, для доказательства того, с чего собственно мы и начали рассуждения.

Итак, эта вторая касательная – не простая прямая, а имеет степень два для переменных x и y (далее, как увидим – степень касательной может быть и 3, и 4, и вообще – n).
Чтобы выделить эти многостепенные касательные на фоне обычных линейных, назовем их Высшими Касательными, сокращенно ВК (то, что это сочетание букв является также моими инициалами – Владислав Кощаков, является случайностью).

Далее мы докажем, что на касательном эллипсе $x_0 x^2 + y_0 y^2 = 1$ точка A не может быть рациональной.
Для этого применим метод, которым без сомнения пользовался сам Пьер Ферма.

-- 13.01.2013, 23:55 --

Третья часть

На широких полях «Арифметики» Диофанта, напротив задачи II-8, находится запись Пьера Ферма на латинском языке:
«Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duas ejusdem nominis fas est dividere; cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet».
В переводе на математический язык:
«Уравнение $x^n + y^n = z^n$ при $n > 2$ неразрешимо»
Я имею «Арифметику» Диофанта («Наука», Москва, 1974), однако там нет оригинального текста Ферма.
А как хотелось бы взглянуть на книгу самого Ферма, почувствовать связь времен…
Предполагаю однако, что экземпляр «Арифметики» Диофанта самого Пьера Ферма не сохранился до наших времен. Увы.

Так вот, задача II-8 гласит: «Заданный квадрат разложить на два квадрата».
Для нас будет значительно полезнее познакомиться со следующей задачей – II-9.
«Данное число, которое складывается из двух квадратов, подразделить на два другие квадрата».
В качестве примера Диофант рассматривает уравнение

$$ x^2 + y^2 = 13 \eqno(9) $$

зная одно рациональное решение которого $\left[ {x_0 = 2;y_0 = 3} \right]$, надо найти второе.
Диофант делает для этого подстановку с новым неизвестным t и параметром k

$$ \left\{ \begin{gathered} x_1 = t + x_0 \hfill \\ y_1 = kt - y_0 \hfill \\ \end{gathered} \right \eqno (10) $$

Подставляя их в исходное уравнение, можно найти это новое неизвестное:

$$ t = \frac{{2ky_0 - 2x_0 }} {{k^2 + 1}} $$

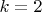
Далее Диофант полагает $k = 2$ (хотя можно выбрать любое другое рациональное значение), после чего легко находит требуемое $\left[ {x_1 = \frac{{18}} {5};y_1 = \frac{1} {5}} \right] $.
Прямой подстановкой найденных значений в исходное уравнение убеждаемся в их правильности.

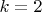
Графически то, что делает Диофант в задаче II-9, выглядит следующим образом. Из точки $A \prime$, симметричной точке A относительно оси OX (он вынужден так поступать, ибо ищет только положительные решения), он проводит прямую с угловым коэффициентом $k = 2$, которая при пересечении c окружностью дает вторую рациональную точку.

Учитывая, что параметр k может иметь любое рациональное значение, получаем веер прямых из точки A, каждая из которых при пересечении с окружностью дает свое рациональное решение. Таким образом, устанавливается взаимно-однозначное соответствие между параметром k и всеми рациональными точками окружности.

Понятно также, что в качестве первоначальной можно выбрать уже полученную точку B, и построить из нее свой веер прямых.
Такие построения справедливы не только для окружности, а для любой кривой второго порядка.
Ферма без сомнения пользовался этим методом.

Воспользуемся и мы с вами, применив его к нашему эллипсу.

Вот его уравнение:

$$ x_0 x^2 + y_0 y^2 = 1 $$

По предположению на нем находится рациональная точка $A\left[ {x_0 ;y_0 } \right]$.
Найдем вторую рациональную точку эллипса, используя для этого подстановки Диофанта.

$$ \left\{ \begin{gathered} x_1 = t + x_0 \hfill \\ y_1 = kt + y_0 = - t + y_0 \hfill \\ \end{gathered} \right \eqno(11) $$

Мы выбрали $k = - 1$ для простоты рассуждений, хотя можно выбрать любое другое рациональное значение.
И вообще, если для $k = - 1$ мы получим что-то необычное для рациональных чисел $\left[ {x_0 ;y_0 } \right]$, то сможем утверждать справедливость полученного результата для любого k (ввиду невозможности выделения какой-либо прямой из всего многообразия пучка прямых – они все равноправны).
Подставляем их в исходное уравнение:

$$ x_0 (t + x_0 )^2 + y_0 ( - t + y_0 )^2 = 1 $$

$$ x_0 t^2 + 2tx_0^2 + x_0^3 + y_0 t^2 - 2ty_0^2 + y_0^3 = 1 \eqno(12) $$

Учитывая, что

$$ x_0^3 + y_0^3 = 1 \eqno(2) $$

упрощаем дальше:

$$ x_0 t^2 + 2tx_0^2 + y_0 t^2 - 2ty_0^2 = 0 $$

Откуда получаем:

$$ t = 2y_0 - 2x_0 \eqno(13) $$

И находим новую рациональную точку B на эллипсе:

$$ \left\{ \begin{gathered} x_1 = 2y_0 - x_0 \hfill \\ y_1 = 2x_0 - y_0 \hfill \\ \end{gathered} \right \eqno(14) $$

Подставляя эти значения в уравнение эллипса, убеждаемся в их правильности.

Но пытливый ум не должен останавливаться на полпути. Давайте-ка попробуем из точки B вернуться обратно в точку A, используя все те же подстановки Диофанта и тот же наклон прямой, соединяющий эти точки.

$$ \left\{ \begin{gathered} x_2 = t_1 + x_1 \hfill \\ y_2 = - t_1 + y_1 \hfill \\ \end{gathered} \right \eqno(15) $$

Действуя аналогично, находим:

$$ t_1 = 2y_1 - 2x_1 \eqno(16) $$

И

$$ \left\{ \begin{gathered} x_2 = 2y_1 - x_1 = 2(2x_0 - y_0 ) - (2y_0 - x_0 ) = 5x_0 - 4y_0 \hfill \\ y_2 = 2x_1 - y_1 = 2(2y_0 - x_0 ) - (2x_0 - y_0 ) = 5y_0 - 4x_0 \hfill \\ \end{gathered} \right \eqno(17) $$

Очень странно!

Ведь мы должны были получить наши первоначальные значения $\left[ {x_0 ;y_0 } \right]$. А получили нечто, не являющееся даже решением уравнения эллипса (получившаяся точка принадлежит другой кривой второго порядка, однако мы не будем развивать здесь это направление, ибо оно уводит нас от обсуждаемой темы).

Для нас важно следующее:

Рациональные точки так себя не ведут!

Наверное, будет логичным сейчас посмотреть на реальный переход из точки A в точку B и обратно для гарантированно рациональной точки A.
Для этого возьмем простейший эллипс:

$$ \frac{{x^2 }} {{1^2 }} + \frac{{y^2 }} {{2^2 }} = 1 \eqno(18) $$

с рациональной точкой $A\left[ {1;0} \right]$.
Делаем подстановку Диофанта:

$$ \left\{ \begin{gathered} x_1 = t + x_0 \hfill \\ y_1 = kt + y_0 \hfill \\ \end{gathered} \right $$

Для упрощения выкладок по-прежнему полагаем $k = - 1$. Можно действовать и в общем виде, для любого k, однако наглядность при этом уступает место многоэтажным дробям, хотя результат будет тем же самым.
Подставляя их в уравнение эллипса, находим:

$$ t = \frac{{2y_0 - 8x_0 }} {5} \eqno(19) $$

Откуда получаем координаты точки B:

$$ \left\{ \begin{gathered} x_1 = \frac{{2y_0 - 3x_0 }} {5} \hfill \\ y_1 = \frac{{3y_0 + 8x_0 }} {5} \hfill \\ \end{gathered} \right \eqno(20) $$

Убеждаемся, что они являются решением для уравнения простейшего эллипса, и отправляемся в обратный путь – из точки B в точку A:

$$ \left\{ \begin{gathered} x_2 = \frac{{2y_1 - 3x_1 }} {5} = \frac{{2(3y_0 + 8x_0 ) - 3(2y_0 - 3x_0 )}} {{25}} = x_0 \hfill \\ y_2 = \frac{{3y_1 + 8x_1 }} {5} = \frac{{3(3y_0 + 8x_0 ) + 8(2y_0 - 3x_0 )}} {{25}} = y_0 \hfill \\ \end{gathered} \right \eqno(21) $$

Вот как должно быть для рациональной точки!

Последовательное применение подстановок Диофанта для рациональных точек на кривых второго порядка с одним и тем же параметром k просто перемещает нас из точки A в точку B и обратно бесчисленное множество раз.
В случае же с касательным эллипсом (7) с каждой попыткой перемещения мы получаем каждый раз новые значения и можно, наверное, обнаружить в этом процессе элементы бесконечного спуска, о котором упоминает Ферма в одном из своих писем.

Отсюда следует, что точка A на эллипсе (7) не есть рациональная. И, соответственно, – на кубике, так как она есть общая точка их касания.
А поскольку мы не накладывали никаких ограничений на выбор точки A на кубике, то это относится к любой ее точке.

Следовательно, на кубике
рациональных точек быть не может!

Вывод достаточно прост и однозначен, и отвечает на вопрос, поставленный в самом начале наших рассуждений.



Автор не только не возражает, но даже считает полезным копирование представленной информации в ваш личный архив для более глубокого ознакомления с ней офлайн (надежность Интернета не равна 100%), а также для сообщения ее, при желании, вашим друзьям, знакомым и другим группам ограниченного числа людей.

[Xaositect]

В формуле (16) $t_1$ найдено неверно. Правильный вывод:
Подставляем $(x_2, y_2)$ в уравнение эллипса:

$$x_0(t_1 + x_1)^2 + y_0(-t_1 + y_1)^2 = 1$$

Раскрываем скобки, группируем

$$t_1^2 (x_0 + y_0) + t_1 (2x_0x_1 - 2y_0y_1) + x_0x_1^2 + y_0y_1^2 = 1$$

Поскольку $(x_1,y_1)$ принадлежит эллипсу, $x_0x_1^2 + y_0y_1^2 = 1$ и

$$t_1 (x_0 + y_0) + (2x_0x_1 - 2y_0y_1)= 0$$

Итого

$$t_1 = 2\dfrac{y_0y_1 - x_0x_1}{x_0 + y_0} = 2(x_0 - y_0)$$

.

[AKM]

Тема перемещена из форума «Великая теорема Ферма» в форум «Карантин»
Тема перемещена в Карантин по следующим причинам: отсутствие аннотации к сюжету.

Исправьте Вашу ошибку и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

Согласно Правилам форума, дискуссионная тема должна быть чётко сформулирована. Чего ради дискутировать о касательных к кубичесокй кривой? Тривиальная задача по аналитической геометрии. Если Вы собираетесь доказывать теорему Ферма, напишите об этом явно в начале сообщения. В начале Вашего длиннющего сообщения.

Vladislav Evg K в сообщении #671292 писал(а):

Докажем, что Пьер Ферма имел право на запись своего знаменитого утверждения на полях «Арифметики» Диофанта.

Это не математическое утверждение, и на аннотацию к теме не тянет.

(Оффтоп)

Vladislav Evg K в сообщении #671292 писал(а):

что хотя стиль изложения и обороты речи в нем могут не соответствовать общепринятым правилам конференции, все же не требовать

Не требуем, раз уж Вы сами не понимаете, что читать это крайне неприятно. Дочитать до конца и узнать, о чём речь, я, например, не смог.
А $x^3+y^3=1$ можно и в уме продифференцировать. Называлось это, кажется, дифференцированием неявной функции.

Vladislav Evg K в сообщении #671327 писал(а):

Значения переменных здесь второй степени, следовательно – это кривая второго порядка.

[Deggial]

Тема перемещена из форума «Карантин» в форум «Великая теорема Ферма»
вернул

[nnosipov]

Vladislav Evg K, Вам понятно, почему Ваша формула для $t_1$ неверна?

Vladislav Evg K в сообщении #671292 писал(а):

Материал, который будет размещен ниже, состоит из четырех небольших частей

Видимо, отсутствующую четвёртую часть автор зарезервировал для извинений перед читателями.

[Vladislav Evg K]

Xaositect, спасибо - ошибка в алгебраических формулах у меня имеется.
Так что от формулы (16) и далее придется все зачеркнуть.
Но до этого места, надеюсь, ошибок не будет найдено.

Главное из того, что было здесь приведено - это возможность замены анализа уравнения

$$x^3 + y^3 = 1$$

на предмет наличия рациональных решений на анализ уравнения эллипса

$$x_0 x^2 + y_0 y^2 = 1\eqno (7)$$

путем введения новых объектов - Высших Касательных.

Придется искать метод бесконечного спуска, который для эллипса будет проще, надеюсь, чем для кубики.

[Vladislav Evg K]

Ничего не понимаю?

Выложен абсолютно новый, достаточно элементарный материал о Высших Касательных, тема относится к разделу дискуссионных на конференции и - полная тишина среди профессионалов.
Я бы сказал - поистине удивительный материал, но такие эпитеты не положены автору, ибо справедлива только оценка со стороны.

Неужели так принято поступать в математической науке?

Я что - напоминаю вам идиота, который доказал теорему Ферма и сам не догадывается об этом, ибо произвести спуск для касательного эллипса может даже студент второго курса математического факультета университета?
К слову - у меня техническое образование.

Дискуссия может отсутствовать только в двух случаях - когда все и так ясно, и когда вообще ничего не понятно.
Остальные случаи дискуссируемы.

[nnosipov]

Vladislav Evg K в сообщении #672057 писал(а):

и - полная тишина среди профессионалов

Вам указали на ошибку в Вашем доказательстве (надеюсь, Вы поняли, в чём она; если нет, я могу подробно объяснить), следовательно, нет и самого доказательства. Пока не появится новый вариант доказательства, обсуждать нечего.

Vladislav Evg K в сообщении #672057 писал(а):

К слову - у меня техническое образование.

Это многое объясняет.

[Алексей К.]

Vladislav Evg K в сообщении #672057 писал(а):

Дискуссия может отсутствовать только в двух случаях - когда все и так ясно, и когда вообще ничего не понятно.

Неверно. Случаев гораздо больше. Данный случай из той категории, когда стиль и манеры автора сразу вызывают отторжение.

[Vladislav Evg K]

Вроде началась дискуссия, но странная какая-то. То стиль автора обсуждаем, то его образование…
А сказать хотя бы что-то по поводу метода Высших Касательных почему-то ни у кого не получается…

Кстати, о стиле.
Знаете, Алексей К., в нем я старался подражать одному из самых моих любимых авторов и моему Учителю – Джорджу Пойя. У меня есть все его книги, даже те, в которых я не все понимаю.
Посмотрите лучшую из них (мое мнение) – «Математическое открытие» М Наука, 1976.
Если такой стиль изложения Вам не нравится, то мне остается только выразить искреннее сочувствие.

Для тех, кто не понял, что здесь происходит, я расскажу чуть более популярно и кратко суть происходящего.
Путем несложного и наглядного способа (см. Вторую часть в начале нашей Темы) введены новые объекты – Высшие Касательные, которые сводят все нечетные степени уравнений ВТФ к анализу одного единственного уравнения (7) – касательного эллипса к кубике (рис.3).
Прием, который использовал сам Ферма и который так долго искали (некоторые даже сошлись во мнении, что он лукавил, что он не имел и не мог иметь доказательства) найден – он перед вами.

И пусть вас не вводит в заблуждение молчание Конференции – наоборот, это является признаком признания полученного результата (иначе бы от метода ВК летели бы сейчас пух и перья от братьев по математическому разуму).
Теорема Ферма доказана на 99,9…%, а анализ уравнения касательного эллипса обязательно кто-нибудь проведет, может даже кто-то из Конференции.

[Someone]

Vladislav Evg K в сообщении #672707 писал(а):

А сказать хотя бы что-то по поводу метода Высших Касательных почему-то ни у кого не получается…

А что о нём говорить-то? Аккуратно докажете теорему Ферма для третьей степени - тогда и будет о чём говорить. А так - мало ли кто какое понятие придумает. Математики их постоянно придумывают в большом количестве. Только у математиков считается неприличным публиковать работу, смысл которой состоит исключительно в придумывании нового понятия. Всегда должен быть результат - решение какой-то задачи с помощью введённого понятия. Причём, либо это должна быть задача, которую без этого понятия никто решить не мог, либо решение было очень сложным, а новое понятие позволило радикально упростить решение. Мы же пока ничего подобного не видим, только термин "высшие касательные". Тем более, что касание кривых - отнюдь не откровение.

[nnosipov]

Vladislav Evg K в сообщении #672707 писал(а):

И пусть вас не вводит в заблуждение молчание Конференции – наоборот, это является признаком признания полученного результата

Да нет никакого результата, есть только глупые заявления и пустые обещания:

Vladislav Evg K в сообщении #672707 писал(а):

Теорема Ферма доказана на 99,9…%, а анализ уравнения касательного эллипса обязательно кто-нибудь проведет, может даже кто-то из Конференции.

[Алексей К.]

Vladislav Evg K в сообщении #672707 писал(а):

...в нем я старался подражать одному из самых моих любимых авторов и моему Учителю – Джорджу Пойя.
......
Если такой стиль изложения Вам не нравится, то мне остается только выразить искреннее сочувствие.

Не надо мне выражать сочувствий. Вы, конечно, при Вашей самоуверенности, с девяткой в периоде уверены, что подражание удалось. Когда чайник пытается подражать профессионалу, в лучшем случае получается пародия.
Да и вообще --- quod licet Jovi, non licet bovi.

[Denis Russkih]

(Оффтоп)

Vladislav Evg K, я совсем недавно был на Вашем месте. Выложил здесь два ошибочных "доказательства" ВТФ, одно за другим.

В своём первом "доказательстве" я тоже, раздуваясь от важности момента, демонстрировал чудеса остроумия и изящной словесности. (Хотя до выражения "Дворец Истины" всё же не додумался. :)) Но в итоге первый же комментатор нашёл в моём "доказательстве" вопиющую ошибку.

Я очень переживал по этому поводу, думал, как же я мог так ошибиться, крутил всё в голове так и эдак... И в какой-то момент моему воспалённому разуму показалось, что я всё-таки нашёл верное решение! Тут же кинулся писать новый пост. Во втором "доказательстве" я уже был более сдержан, старался высказываться коротко и по существу. (Но всё равно в конце не утерпел и ещё раз всем напомнил, какой важный результат мною получен. :)) Разумеется, и это "доказательство" было очень быстро разгромлено. Вновь оказалось, что я упустил из виду очень важный момент.

Сейчас жгучий фейспалм охватывает моё лицо, когда я вспоминаю об этих двух самонадеянных попытках. При этом я почти не стыжусь своих дилетантских рассуждений, ведь я и не мог выдать ничего иного на своём уровне понимания проблемы. Но мне очень стыдно за шапкозакидательные настроения, за свою снисходительную уверенность в том, что я нашёл элементарное решение, которое проглядели умники со всего мира. :) И особенно мне стыдно за то, как я старался доступно и с юмором изложить свои простенькие мысли, как бы готовя их к размещению в учебнике истории. :)

Мой вам искренний совет, отложите пока в сторону этот замечательный стиль, в котором писал Джордж Пойя — скажем, до тех пор, пока Вы не достигнете очень значимых результатов, и Вас не попросят написать книгу о своём открытии. :) А если Вам кажется, что важные результаты уже достигнуты, то надо всё же потерпеть с распусканием хвоста хотя бы до того момента, когда и другие люди признают Ваши заслуги.

Мне почему-то кажется, что даже сам Джордж Пойя, если бы ему вдруг пришло в голову доказательство ВТФ, вряд ли стал бы излагать его перед специалистами в том же стиле, в котором писал научно-популярные книги. (И в любом случае, Вы-то ведь не Джордж Пойя.)