Совместными усилиями с горем пополам получилось у нас вот что:
Формула коэффициента корреляции выглядит вот так:

Отсюда формула ковариации:

Отсюда

т.к. математическое ожидание симметрично распределенной величины равно нулю, т.к. это интеграл от нечетной функции с симметричным относительно нуля пределами интегрирования. След-но второе слагаемое "зануляется".
Первое слагаемое если его считать равно:

Рассмотрим что здесь есть что:

симметрично, следовательно является четной функцией.

тоже четная функция. А

нечетная. Следовательно первое слагаемое тоже равно нулю. Тогда ковариация
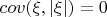
. Следовательно:
