a) тривиально.
Пусть

. Тогда

Если

нечетное, то ничего доказывать. Случай

исключается вычеркиванием не нужных нулей с конца.
При

случаи

тривиальны, в случае

вторые цифры

нечетны.
b) В случае

остается рассмотреть только случай

(

заканчивается на 4).

, Следовательно

заканчивается на 32 при

и на

.
Остается проверять только

/ В этом случае

. Вторая цифра

влияет только на третью с конца цифру, но не меняет четность для

,

и далее влияют только на четвертую с конца цифру. Это доказывает
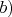
.