1. Это число способов можно грубо, но довольно просто оценить.
Обозначим наше число

. Очевидно, что наибольшее значение суммы

аликвотных дробей (если не считать

таковой) равно

, где

. Но

(


постоянная Эйлера-Маскерони), поэтому при

искомое число способов равно 0.
Наименьшее значение суммы

аликвотных дробей со знаменателями, не превышающими

, равно

. Но

, поэтому наибольшее значение

(обозначим его

) равно

, где
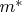

(положительный) корень уравнения

. Следовательно, искомое число способов не превышает

.