доказать полноту

[vlad_light]

Никогда такое не доказывал, поэтому "стандартный подход" подойдёт.
Нужно доказать, что пространство всех последовательностей $\mathbb R^\infty $ с метрикой $d(x,y)=\sum\limits _{n=1}^\infty \frac{1}{2^n}\frac{|x_n-y_n|}{1+|x_n-y_n|} $ полно.

[statistonline]

http://dxdy.ru/topic62564.html

[vlad_light]

Проверьте, пожалуйста:
$d_e(x,y):=|x-y|$ - евклидова метрика. Рассмотрим пространство $(\mathbb R, d_e)$ - оно является полным, соответственно любая фундаментальная последовательность в нём имеет предел. Пускай $\{x^{(n)},n\geq 1\}$ - последовательность из $\mathbb R^\infty$. Тогда

$$d(x^{(n)},x^{(m)})=\sum\limits _{k=1}^\infty \frac{1}{2^k}\frac{|x^{(n)}_k-x^{(m)}_k|}{1+|x^{(n)}_k-x^{(m)}_k|}=\sum\limits _{k=1}^\infty \frac{1}{2^k}\frac{d_e(x^{(n)}_k,x^{(m)}_k)}{1+d_e(x^{(n)}_k,x^{(m)}_k)}$$

при каждом фиксированом $k$ выполняется $d_e(x^{(n)}_k,x^{(m)}_k)<\varepsilon$ при достаточно большие $n$ и $m$. Следовательно, последняя сумма меньше, чем

$$\sum\limits _{k=1}^\infty \frac{1}{2^k}\frac{\varepsilon}{1+\varepsilon}=\frac{\varepsilon}{1+\varepsilon}\to 0, \varepsilon \to 0$$

[g______d]

vlad_light в сообщении #626556 писал(а):

при каждом фиксированом $k$ выполняется $d_e(x^{(n)}_k,x^{(m)}_k)<\varepsilon$ при достаточно большие $n$ и $m$. Следовательно, последняя сумма меньше, чем

$$\sum\limits _{k=1}^\infty \frac{1}{2^k}\frac{\varepsilon}{1+\varepsilon}=\frac{\varepsilon}{1+\varepsilon}\to 0, \varepsilon \to 0$$

Вы сначала говорите, что при каждом фиксированном $k$, а в последующей оценке используете равномерность по всем $k$, которой может не быть. Нужна ли она? Рассмотрите отдельно первые $k_0$ членов, а "хвост" оцените грубо.

[vlad_light]

Хорошо. Тогда делаем так: берём первые $K$ и делаем для каждого оценку $d_e(x^{(n)}_k,x^{(m)}_k)<\varepsilon _k$, а всю сумму оцениваем через $\varepsilon _K:=\max\limits _{k=\overline{1,K}}\{\varepsilon _k\}$ -- получится что-то типа равномерной оценки... А в хвосте мы вон ту дробь оценим $1$ сверху и получим хвост ряда из обратных степеней двойки, который сам по себе сходящийся, соответственно хвост стремится к $0$.
Как теперь? По-моему, всё ок

[vlad_light]

Ещё одна задачка: показать, что $l^p, 1\leq p\leq \infty$ - борелевское множество в $\mathbb R^\infty$. Я знаю, что цилиндр (множество таких последовательностей из $\mathbb R^\infty$, у которых первые $n$ координат фиксированы) является борелевским множеством. Как Эль-пэ свести к цилиндру?

[Oleg Zubelevich]

vlad_light в сообщении #626673 писал(а):

Ещё одна задачка: показать, что $l^p, 1\leq p\leq \infty$ - борелевское множество в $\mathbb R^\infty$. Я знаю, что цилиндр (множество таких последовательностей из $\mathbb R^\infty$, у которых первые $n$ координат фиксированы) является борелевским множеством. Как Эль-пэ свести к цилиндру?

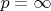
Покажем, что замкнутый шар $B_r$ пространства $l^p,\quad p\in(1,\infty]$ замкнут в $$\mathbb R^\infty$. Для $p=\infty$ это очевидно. Докажем для остальных.

Пусть $x_n\in B_r$ сходится в $\mathbb R^\infty: \quad x_n\to x.$ Отсюда следует, что для всякого финитного элемента $\psi\in l^{p'}$ выполнено $(x_n,\psi)\to(x,\psi).$
По теореме Банаха-Штейнгауза $x_n\to x$ -- слабо в $l^p$. Т.к. шар слабо занмкнут в $l^p$ получаем $x\in B_r$.
Теперь пространство $l^p,\quad p>1$ является борелевским множеством как объединение счетного числа замкнутых шаров.