4. Если

и

представимы в виде суммы двух квадратов, то из тождества

следует, что и

представим.

Поскольку первый множитель разложим на сумму двух квадратов, достаточно рассмотреть второй множитель.
При

разложение тривиально
Если же

, то невозможность разложения на сумму двух квадратов покажет рассмотрение остатков при делении на
 -- Вт авг 07, 2012 17:24:12 --
-- Вт авг 07, 2012 17:24:12 --3a. В случаях

и

получаем тривиальные решения.
При

сумма в левой части делится на

и не делится на

. Откуда
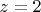
. Но при

левая часть оканчивается на

и квадратом быть не может. Перебором при

получаем единственное нетривиальное решение

.