Ну и ладно, у вас гораздо проще вариант.
-- Пн июл 30, 2012 16:12:45 --б) можно тоже.
Да и вообще любое количество можно:
располагаем на двух вложенных окружностях по
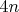
вершин, так чтобы из каждой точки на внешней окружности можно провести стороны к

различным парам соседних точек внутренней. Это даст

зубчатых многоугольников с несовпадающими сторонами.