Я решил назвать эту тему: "Введение в математическую логику".
Первая версия этого введения не является удовлетворительной, потому что не основана на стандартном
формальном математическом языке: логике первого порядка.
С другой стороны, логика первого порядка является только ядром, недостаточным для формализации
математики.
Примером более полного формального языка, основанного на логике первого порядка является язык "Мицар".
После ознакомления с этим языком, я начал писать вторую версию этого введения.
========================================================================================================
Введение в математическую логику.
Математика занимается определением вводимых понятий, формулировкой утверждений и доказательством их истинности.
Доказательство это убедительное рассуждение, которое, при необходимости, можно перевести на формальный язык.
Формальный язык отличается от обычного тем, что существует автоматическая процедура (алгоритм), позволяющая проверять правильность записанного на этом языке математического текста.
Перевод математического текста на формальный язык редко осуществляется на практике, обычно достаточно понимания, что такой перевод возможен.
Логическим доказательством называется последовательное применение правила логического вывода

, которое позволяет вывести истинность некоторого утверждения

из истинности двух других утверждений

и "если

, то

".
Правило вывода применяют один или более раз, до тех пор, пока ни будет получено доказываемое утверждение.
Поскольку доказательство опирается на уже известные истины, то первоначальные истины доказать невозможно.
Утверждения, принимаемые за истину без доказательства, называются аксиомами.
Аксиомы не нуждаются в доказательстве по той причине, что они являются определением вводимых понятий и
математических теорий в целом.
Система аксиом математической теории (и сама теория) нызывается противоречивой, если в ней можно доказать некоторое утверждение

и его отрицание "не

".
Система аксиом математической теории (и сама теория) называется полной, если любое утверждение теории можно или доказать или опровергнуть.
В идеале, система аксиом математической теории должна быть непротиворечивой и полной, но этот идеал недостижим.
Если теория достаточна для того, чтобы в ней можно было определить арифметику, то утверждение о непротиворечивости теории невозможно доказать в рамках этой теории.
Утверждение о непротиворечивости теории можно перевести на язык арифметики, и, в таком виде, оно не следует из аксиом теории.
Поэтому, если такая теория непротиворечива, то она не является полной.
Это доказал австрийский математик Курт Гёдель в 1931 году.
Из теоремы Гёделя не следует, что нельзя доказать непротиворечивость арифметики никаким способом.
Доказательства непротиворечивости арифметики имеются в теории множеств.
Математические рассуждения обычно не являются формальными.
Но возможность перевода математических рассуждений на формальный язык не должна исчезать из вида.
Для этого требуется знание основ математической логики и теории множеств, которые лежат в основании математики.
Цель этого введения познакомить читателя с элементами формальной математической логики.
Математические понятия.
В любой математической теории есть первоначальные понятия, которые, в силу своей первоначальности, не определяются через понятия, введённые ранее.
Первоначальным понятиям даётся интуитивное и формальное определение.
Интуитивное определение описывает смысл первоначальных понятий и их свойства, лежащие в основе формального определения.
Формальное определение первоначальных понятий даётся в форме аксиом.
Непервоначальным понятиям даются определения через понятия введённые ранее.
Любые математические понятия, как первоначальные, так и не первоначальные записываются с использованием переменных.
Понятия, как и выражения, которые из них образуются, имеют тип объекта или утверждения.
Например, понятие "

" имеет тип объекта, а понятие "

имеет тип утверждения.
Переменные тоже имеют тип объекта или утверждения, в частности в приведённых понятиях,

и

- переменные типа объекта.
Переменные объекты обозначаются латинскими буквами, возможно с индексами, например

.
Переменные утверждения обозначаются греческими буквами, например,

.
В некоторых формальных математических языках, для обозначения переменных утверждений используются не греческие, а латинские буквы.
В этом случае переменные объекты и переменные утверждения обозначаются различными наборами латинских букв или же различаются с помощью специальных правил.
В математике, иногда, используются переменные, содержащие другие переменные, например,

.
Такие переменные называются переменными с аргументами.
Переменные с аргументами случаются в математических выражениях, но в математических понятиях они не используются.
Переменные типа объекта без аргументов называются объектными переменными.
Переменные типа объекта с аргументами называются функциональными переменными.
Переменные типа утверждения называются предикатными переменными.
В математических понятиях используются только объектные переменные и предикатные переменные без аргументов.
В математике есть стандартный формальный язык, который называется логикой первого порядка.
Математические понятия записываются на языке логики первого порядка в следующей форме:

, где

- так называемый функциональный или предикатный символ, а

- объектные переменные.
Например, понятие

записывается на языке логики первого порядка в форме

, где

- функциональный символ.
В других формальных языках есть различные формы записи математических понятий, и форма

является одной из них.
В логике первого порядка нет предикатных и функциональных переменных, что делает её недостаточной для формулировки стандартных математических теорий.
В логике второго порядка есть предикатные и функциональные переменные, но это более сложный формальный язык.
Чтобы избежать этой сложности, к логике первого порядка добавляют предикатные и функциональные переменные, но их использование носит ограниченный характер.
Наличие предикатных переменных в расширенной логике первого порядка позволяет определить её как любую другую математическую теорию при помощи первоначальных понятий и аксиом.
Следующие понятия являются первоначальными в логике:
1. Логические связки: "не", "и", "или", "если ... то ...", "тогда и только тогда, когда"
2. Логические выражения: "существует" и "для любого"
3. Знак равенства:

.
В записи с переменными, эти понятия имеют вид:
1. не

,

и

,

или

, если

то

,

тогда и только тогда, когда

,
2. для любого

, существует

,
3.

,
где

и

- объектные переменные, а

и

- предикатные переменные.
Мы привели не все логические связки, а только основные.
Удобно считать все логические связки первоначальными понятиями, хотя одни можно определить через другие.
Логические понятия имеют специальные обозначения, например,

(и),

(если ... то ..., из ... следует ...),

(тогда и только тогда, когда),

(cуществует),

(для любого).
Из других обозначений отметим непервоначальное понятие

(существует единственный).
В любой математической теории, кроме логики, речь идёт не о любых, а о специфичных объектах, поэтому вводят одно или несколько первоначальных понятий, именующих объекты теории.
Например, в арифметике вводят понятие натурального числа, в геометрии - понятия точки и прямой, а в теории множеств понятие множества.
Эти понятия имеют вид:
a)

- натуральное число
б)

- точка,

- прямая
в)

- множество
В стандартной теории множеств можно обойтись без именующих понятий, поскольку в ней все объекты являются множествами.
Но можно и ввести понятие множества, поскольку оно используется в обычном математическом языке.
Приведём примеры других математических понятий (не обязательно первоначальных):
А)

Б)

- целое число,

делится на

,

- чётное число
В)

При определении понятия следует указать его область определения (для каких значений переменных оно определяется).
Например, понятие

определяют сначала для целых неотрицательных чисел, затем для целых чисел, включая отрицательные.
Если допускаются произвольные значения переменных, то понятие не имеет области определения.
Логические и именующие понятия не имеют области определения.
Область определения понятия указывается при его определении.
В дальнейшем, при использовании понятия в выражениях, область определения обычно указывается до или после выражения.
Например: пусть

, где

и

- целые числа.
Математические выражения.
Приведём примеры математических выражений:
1)

2)

, для любого

3)

4)

,

-чётное число
5)

, если

то

6)

или (не

), если (

и

) то (

и

)
Начальными выражениями являются первоначальные понятия.
Новые выражения образуются подстановкой одних выражений в другие вместо свободных переменных.
При этом, заменяемая переменная и подставляемое выражение должны быть того же типа (объект или утверждение).
Можно также получать новые выражения заменяя одни переменные другими.
Например, можно получить выражение

из понятия

.
Заменяя переменную без аргументов переменной с аргументами, можно получить выражения с предикатными и функциональными переменными.
Математическое утверждение со свободным объектным переменным называется выражением свойства, с двумя или более объектными переменными - выражением отношения.
Математический объект со свободными объектными переменными называется выражением функции.
Выражения без свободных переменных называются постоянными.
Выражения 1) являются постоянными объектами, 2) - постоянными утверждениями, 3) - выражениями функций, 4) - выражениями свойств, 5) - выражениями отношений.
Математические утверждения со свободными объектными переменными называются предикатами.
Выражения свойств и отношений являются предикатами.
Аксиомы и аксиомные схемы.
Аксиомы задаются выражениями типа утверждения, в которых могут быть свободные объектные переменные.
Смысл аксиом со свободными переменными заключается в их истинности для любых значений свободных переменных.
Например, смысл аксиомы

выражается утверждением: "для любого

".
В логике первого порядка есть специальное правило вывода, позволяющее вывести последнее утверждение из первого.
Из последнего утверждения можно вывести утверждения

и т.д. используя одну из аксиом логики первого порядка.
Аксиомной схемой называется выражение с одной или более предикатной переменной, которое становится аксиомой, при подстановке вместо предикатной переменной конкретного предиката.
Таким образом, аксиомная схема порождает бесконечное множество аксиом.
Например, выражение "если

то

" с предикатной переменной

является аксиомной схемой.
Если вместо

подставить, например, предикат
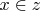
, получится аксиома "если

то

.
В предикатной переменной

выделена объектная переменная

, которая должна быть свободной в подставляемом вместо

предикате.
Вместо выражения

подставляется тот же предикат, в котором переменная

заменена на переменную

.
Подставляемый предикат не должен содержать предикатных и функциональных переменных, но может содержать другие свободные объектные переменные, кроме выделенной переменной

.
Присутствие выделенной переменной

в подставляемом предикате не является обязательным.
Например, можно вместо

подставить предикат

или даже постоянное утверждение

.
Вообще, в логике первого порядка формализм начинается после замены предикатной переменной подставляемым выражением, и при формулировке аксиомной схемы можно указать специальные правила подстановки.
В других формальных математических языках предикатные и функциональные переменные являются частью формализма.
Среди таких языков выделяется язык "Мицар", который основан на расширенной логике первого порядка и позволяет осуществлять компьютерную проверку математических доказательств.
Язык "Мицар" близок к обычному математическому языку, и на этом языке написано большое количество проверенных компьютером доказательств.
Определения и аксиомы определения.
Математические понятия, не являющиеся первоначальными, вводятся определениями, выражающими эти понятия через уже известные.
На формальном языке, определения выражаются аксиомами, которые являются утверждениями, верными "по определению".
Эти аксиомы называются аксиомами определения.
Аксиомы определения бывают двух видов, в зависимости от типа определяемого понятия (объект или утверждение).
Примером аксиомы определения утверждения является выражение:
"

-чётное число

делится на

",
определяющее понятие чётного числа через понятие делимости на

.
Аксиома определения утверждения имеет вид:

, где

- определяемое понятие типа утверждения, а

- определяющий предикат с теми же свободными переменными, что и

.
Примером аксиомы определения объекта является выражение:
"


(

и

) или (

и

)",
определяющее понятие наименьшего числа из двух чисел

и

.
Аксиома определения объекта имеет вид: "

, где

- определяемое понятие типа объекта,

- переменная не содержащаяся в

, а

- определяющий предикат с теми же свободными переменными, что и "

".
Можно давать аксиому определения объекта и в виде:

.
При определении объекта должно выполняться следующее условие: "существует единственный

".
Это условие, которое называется условием определения объекта, должно быть доказано перед принятием определения.
В некоторых формальных математических языках, например, в языке "Мицар", доказательство условия определения объекта является необходимой частью определения.
Продолжение следует.