Пожалуйста, помогите решить задачу про турнир шашек! :-)

[romlit]

Люблю олимпиадную математику) вызвала интерес вот такая вот задачка... может, кто-нибудь знает ее решение? "Несколько учащихся 9А и 9Б классов организовали турнир по шашкам. Каждый участник турнира сыграл с каждым по одной партии. За выигрыш присуждали 2 очка, за ничью - 1 очко, за проигрыш - 0 очков. Учащиеся 9А класса вместе набрали 26 очков, а учащиеся 9Б класса, которых было на 3 больше, набрали очков поровну. Сколько было участников турнира?"

[MrDindows]

Пусть в А классе $x$ учеников. Тогда в Б классе $x+3$. Всего их $2x+3$, значит было сыграно $\frac{(2x+3)(2x+2)}{2}$ игр. С учётом того, что за каждую игру, вне зависимости от результата участники получают в сумме 2 очка, то всего было получено $(2x+3)(2x+2)$ очка. И если у учеников класса А в сумме $26$ очков, то у учеников класса Б $(2x+3)(2x+2)-26$
Из условия задачи следует что $(2x+3)(2x+2)-26=(x+3)(4x-2)-14$ делится на $x+3$, а значит и $14$ делится на $x+3$, откуда $x$ равен либо 11, либо 4. Осталось проверить оба варианта.

[Dave]

Ответ: 11

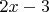
Пусть из 9Б было $x$ участников. Тогда из 9А было $x-3$ участников. Всего было $2x-3$ участника и набрано $(2x-3)(2x-4)$ очков. Пусть каждый из 9Б набрал $y$ очков. Общее количество очков, набранных учениками 9Б не может быть больше суммы чисел $x(x-1)$ (очки в играх между собой) и $2x(x-3)$ (очки в играх между учениками разных классов). Получаем такую систему:

$$\begin{cases} 26+xy=(2x-3)(2x-4),\\ xy \leqslant x(x-1)+2x(x-3). \end{cases}$$

Из первого уравнения получаем: $y=4x-14-\frac {14} x$. Учитывая, что $x$ и $y$ - целые числа, причём $x>3$, получаем две пары решений $(x,y)$: $(7,12)$ и $(14,41)$. Неравенство исключает вторую пару. Значит $x=7$.

[MrDindows]

Dave в сообщении #565114 писал(а):

Всего было $2x-3$ участника и набрано $(2x-3)(2x-2)$ очков.

По-моему, вы ошиблись с количеством очков)

[romlit]

MrDindows в сообщении #565112 писал(а):

Пусть в А классе $x$ учеников. Тогда в Б классе $x+3$. Всего их $2x+3$, значит было сыграно $\frac{(2x+3)(2x+2)}{2}$ игр. С учётом того, что за каждую игру, вне зависимости от результата участники получают в сумме 2 очка, то всего было получено $(2x+3)(2x+2)$ очка. И если у учеников класса А в сумме $26$ очков, то у учеников класса Б $(2x+3)(2x+2)-26$
Из условия задачи следует что $(2x+3)(2x+2)-26=(x+3)(4x-2)-14$ делится на $x+3$, а значит и $14$ делится на $x+3$, откуда $x$ равен либо 11, либо 4. Осталось проверить оба варианта.

Правильный ответ 11! Дело в том, что мое решение было идентично Вашему, но я не стал решать Ваше последнее уравнение... засомневался...решил, что перебором тут не надо решать... а нужно получить готовый ответ из системы уравнений...спасибо Вам))) буду смелее в следующий раз)

-- 28.04.2012, 21:01 --

Друзья!!! Спасибо Вам всем)))