О происхождении комплекта.Эти задачи являются последовательными шагами решения задачи #4 11-го класса с LII Всеукраинской Математической Олимпиады (26–30 марта 2012, Кировоград):
 — такая треугольная пирамида, что для
— такая треугольная пирамида, что для  — точки пересечения медиан грани
— точки пересечения медиан грани  выполняются неравенства:
выполняются неравенства: 
Доказать, что 
При решении естественно свести задачу к какому-то простейшему случаю, для которого и доказать неравенство.
Не уменьшая общности можно считать, что наименьшее из расстояний

это

Зафиксируем точки

и

, и подвигаем точки

и
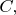
так, чтобы сумма расстояний

уменьшилась. Условие неподвижности точек

и

означает, что середина отрезка

при движении точек сохраняется. Сумма расстояний

уменьшается независимо от положения точки

в том случае, если точки

и

приближаются к середине отрезка (
задача #1 из комплекта). При этом всегда можно добиться чтобы меньшее из расстояний

стало равняться

(Не уменьшая общности можно считать, что это

) В результате треугольник

становится равнобедренным (

).
Теперь поищем для точки S такое место, чтобы сумма расстояний |SA|+|SB|+|SC| была поменьше.
/Конечно, можно сразу послать её в точку Торричелли, но… "мы пойдём другим путём", поскольку "нормальные герои всегда идут в обход".
Во-первых, далеко не все школьники знают, что такое точка Торричелли.
Во-вторых, решение с использованием точки Торричелли может быть не засчитано (т.к. свойства этой точки — далеко не школьный материал)./Очевидно, что все 3 расстояния уменьшатся, если спроектировать (ортогонально) точку

на плоскость

Но гонять точку по всей плоскости не очень удобно, поэтому поищем для неё более подходящее место. Легко заметить, что если точку

(проекцию точки

на плоскость

) двигать параллельно

, то и

и

будут наименьшими тогда, когда эта точка попадает на высоту

(
задача #2 из комплекта).
Остаётся показать, что для любой точки
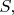
лежащей на высоте

Введём угол

Тогда

Обозначим

Тогда неравенство

принимает вид

или, учитывая что

произвольное, большее 1,

(
задача #3 из комплекта).
--------------------------------------------------------------------------
Статистика по этой задаче.Всего участвовало 45 одиннадцатиклассников.
Результаты по задаче (максимум — 7 баллов):
7 баллов — 1 участник;
5 баллов — 1 участник;
3 балла — 1 участник;
0 баллов — 42 участника.








