Нехаусдорфово пространство T1

[Human]

Здравствуйте.
Я недавно начал изучать топологию и сейчас добрался до аксиом отделимости. Естественно возникло желание придумать примеры пространств $T_i$, которые не являются пространствами $T_{i+1}$. И если для $i=0$ все просто, то в случае $i=1$ я оказался в затруднении. В интернете нашёл только упоминание топологии Зарисского, но я, похоже, не готов к её пониманию Просидев порядка 4 часов, вроде бы что-то придумал, поэтому прошу проверить и указать на ошибки.

Рассмотрим топологическое пространство $(X, \tau)$, где $X=\mathbb N$, а $\tau=\{\varnothing, \mathbb N, \mathbb N\setminus A\}$, где $A\subset\mathbb N, |A|<+\infty$. Другими словами, в топологии находятся всевозможные разности множества натуральных чисел с любым его конечным подмножеством, плюс пустое множество. Это семейство является топологией, так как

1) Все множество $X$ и пустое множество там лежит;

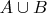
2) $(\mathbb N\setminus A)\cap(\mathbb N\setminus B)=\mathbb N\setminus(A\cup B)\in\tau$, так как множество $A\cup B$ конечно;

3) $\bigcup\limits_{i\in I}\mathbb N\setminus A_i=\mathbb N\setminus(\bigcap\limits_{i\in I} A_i)\in\tau$, так как $\bigcap\limits_{i\in I} A_i$ конечно.

В этом пространстве любые два непустых открытых множества пересекаются по непустому (счётному) подмножеству, поэтому это пространство не хаусдорфово. С другой стороны для любых пар чисел $k,m$ существует окрестность числа $k$ вида $\mathbb N\setminus\{m\}$, в котором число $m$ не лежит, значит это пространство $T_1$.

И ещё вопрос по терминологии: я так понял, что пространства $T_3$ и $T_4$ называются соответственно регулярным и нормальным, если они также являются пространствами $T_1$, верно? Просто в некоторых источниках это условие опускают и считают, что пространства $T_3$ и регулярное эквивалентны (аналогично с $T_4$ и нормальным).

[apriv]

Human в сообщении #550982 писал(а):

Другими словами, в топологии находятся всевозможные разности множества натуральных чисел с любым его конечным подмножеством, плюс пустое множество.

Ага. Это, кстати, и есть частный случай топологии Зариского, с точностью до одной точки.

[Human]

apriv
Спасибо за ответ.
Забавно получилось, всё равно всё свелось к топологии Зарисского. Может быть когда-нибудь наберусь смелости и разберусь в ней...

Можете ещё как-то прокомментировать мой последний вопрос (не этот ), какие определения сейчас более распространены? Мне кажется, что раз уж без требования аксиомы $T_1$ не обойтись при обосновании регулярности нормального пространства и хаусдорфовости регулярного пространства, то стоит различать пространства $T_3$ и регулярное (аналогично $T_4$ и нормальное).

[wallflower]

Наиболее употребимая русская терминология:
регулярное = $T_1+T_3$
нормальное = $T_1+T_4$

В западной литературе бывают вариации. Например, normal space -- это наше $T_4$, а $T_4$ space -- это наше нормальное. Короче, нужно использовать терминологию той литературы, которую читаете.

Множество контрпримеров (в том числе всяких "$T_{k}$, но не $T_{k+1}$") есть в книжке "Элементарная топология" Виро и др.

[Human]

wallflower
Ясно. Спасибо за книгу.