Не подскажите существует ли
оптимальный алгоритм разбиения произвольной матрицы
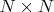
на равные сегменты. Примерно вот так:

Здесь показан один итерационный шаг, поскольку матрица небольшая. Дальнейшее разложение бессмысленно, поскольку дальше идут отдельные элементы матрицы. Задача достаточно проста, если

кратно степени 2-ки. Результатом алгоритма будет серия

, здесь

(размер элементарной ячейки=матрицы минимального размера). А если нет? Хотелось бы узнать, существует ли доказанный оптимальный алгоритм такого разбиения. И как быть в случае нечётного

. Скорее всего необходимо выбирать размер элементарной ячейки соответствующий и наверно будут существовать матрицы, которые не могут быть оптимально разбиты на равные части. Тогда второй вопрос: существует ли алгоритм разбивающий матрицу с минимальными потерями начальных ограничений?