wallflower(Оффтоп)
Странно, что у нас почти в одно время возник один и тот же вопрос.
Кстати, где Вы встретили поле множеств?
И еще кстати, кольцо с единицей -- это не поле, вообще говоря.
Спасибо. Получается, что алгебра множеств

-- это булева алгебра
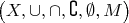
.
Относительно полуколец и

-алгебр вопрос пока остается открытым.
-- 12.03.2012, 01:29 --Сигма алгебра алгебраической системой не является, т.к. в ней имеется "бесконечноместная операция".
Хорошо, тогда вопрос про

-кольца и

-алгебры снимается.
(Оффтоп)
Но все равно интересно почему именно

, а не, например,

или еще что-нибудь? Неужели

исторически символизирует счетность, типа как

символизирует малое число?
Остаются тогда только полукольца. Пока не могу сообразить, что там будет операцией сложения.