

А как дальше, что можно сделать? Напрашивается только немонотонное внесение под дифференциал

. Но ведь так нельзя?
-- 03.03.2012, 18:33 --А можно ли проделывать такой трюк?
Допустим мы хотим взять

Рассматриваем неопределенный интеграл

Заменой

вычисляем его, возвращаемся к переменной

и получаем

Можно ли сказать, что

?
(уже неактуально)
Можно ли сделать так, чтобы интеграл выглядел красиво с одним долларом (в строчке, а не центрированно)? Или только с двумя можно?
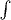
-- как-то не эстетично. Красиво

Код:
$\displaystyle\int$

Спасибо, исправил теперь!