По поводу примера четырёх функций чуть усложню задачу:
1) Все функции должны быть записаны в явном виде.
2) Они должны быть неограничены сверху и снизу, кроме случая +1+2+3-4, в котором неограниченность требуется только снизу.
3) Для случая +1-2+3+4 функция должна дополнительно удовлетворять условию

при всех целых

.
Руст, Вы погорячились. Условие п.3. говорит о неотрицательности

только при

. Никто не утверждает, что

.
hippie указал все подходящие функции. Когда я думал о том, как логичнее записывать их через параметр, то пришёл к выводу, что лучше так:
![$$f(x)=t\left[\frac x t \right],$$ $$f(x)=t\left[\frac x t \right],$$](https://dxdy-02.korotkov.co.uk/f/d/7/5/d754fc3cf9220ba6a2f9612a7d5258dd82.png)

, тогда

означает скачок на графике (как по

, так и по

). Случай

- предельный при
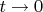
.
hippie, мне интересно, как Вы получили, что:
1)

;
2)

принимает все действительные значения в I случае;
3)

во II случае?