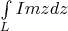
где

окружность
в задании сказано, что нужно пользоваться формулой для вычисления интеграла от фкп при заданном пути интегрирования
я предполагаю, что нужно сделать что-нибудь следующее:

тогда
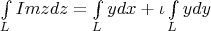
ещё можно, в принципе, параметрически задать контур:


верны ли мои рассуждения? что делать дальше?