Пусть полином

с целыми коэффициентами имеет минимум три различных целых корня
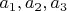
. Тогда его можно представить в виде

, где

- многочлен с целыми коэффициентами. Значит если какой-либо

имеет хотя бы один целый корень

, то

, т.е.

, причём число

- целое, как и числа

. Но это означает, что все сомножители равны

, поэтому минимум два из чисел

равны. Берём их разность и получаем, что

при

, а это противоречит предположению о различности этих чисел.
-- 25.12.2011, 20:19 --Естественно, в условии должно звучать, что корни различны, я так и предполагал с самого начала. Иначе (т.е. когда корни считаются с учётом кратности) утверждение неверно, взять хотя бы

.