при
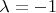
берем

чтобы компоненты были целочисленные и получаем (3,3,-4), а если взять 8 то будет (6,6,-8) как тут
У Вас тут совершенно ничего невозможно понять. Во-первых, собственный вектор, предложенный Вами в стартовом посте, совершенно явно не является собственным. Во-вторых, Ваши ссылки ведут либо на какие-то другие матрицы, либо вообще не пойми куда.
Чётко перепишите ещё раз: свою матрицу, собственный вектор и присоединённый. Затем матрицу откуда-нибудь оттуда, предлагаемый там собственный вектор и предлагаемый присоединённый. Тогда можно будет хоть что-то обсуждать.
И в любом случае Вы должны понимать, что присоединённый вектор определяется сильно неоднозначно по двум причинам. Во-первых, собственный вектор в правой части системы определён лишь с точностью до постоянного множителя. Но и даже если его зафиксировать -- в любом случае к уже найденному присоединённому вектору можно безнаказанно добавить любой собственный; это -- дополнительный эффект.