Интеграл

[Stotch]

Подскажите пожалуйста вот мне дан интеграл

$$\int_{0}^{\pi} sin(2x)sin(nx) dx$$

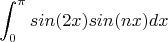
вот я раскладываю призведение синусов на сумму косинусов

$$\int_{0}^{\pi} cos(x(2-n))dx+\int_{0}^{\pi} cos(x(2+n)) dx$$

там 1/2 еще,n от 1 до беск.Я говорю предподу что он=0 всегда.Он говорит что нет.ПОЧЕМУ НЕТ????при каких n он не будет=0 и почему????

-- Пн дек 12, 2011 12:38:49 --

ведь внося косинус под дифферинциал там потом при 0 и при пи всегда получается 0.В чем я не прав???

[bot]

Stotch в сообщении #514655 писал(а):

при каких n он не будет=0

Например для n=2.

[Stotch]

почему???мы ведь когда вносим под дифферинциал получаем синус(0)=0 так???

[Joker_vD]

Ну-ка покажите, как вы под дифференциал вносите.

[Stotch]

$$\int_{0}^{\pi} cos(x(2-n))dx=\frac{1}{2-n}\int_{0}^{\pi} d(sin(x(2-n)))$$

так???
а при n=2 интеграл=бесконечости????или пи???и почему

[Joker_vD]

Я не знаю, рассказывали вам или нет, но $\cos(0x)=\cos0=1$, а интеграл $\int\limits_0^\pi 1\,dx$ равен, как ни странно, $\pi$.

Stotch в сообщении #514667 писал(а):

а при n=2 интеграл=бесконечости????или пи???

Вот вы же видите, что при $n=2$ такое внесение незаконно. Нет, все равно вносите, а потом думаете: "что бы это могло значить?"

[Stotch]

тюе изначальный интеграл мой=0 при всех n кроме 2??а при n=2 он равен пи???

[bot]

Нет

Stotch в сообщении #514655 писал(а):

там 1/2 еще