Видимо,

здесь целое число, и речь идёт об отношении делимости в кольце
![$\mathbb{Z}[\omega]$ $\mathbb{Z}[\omega]$](https://dxdy-02.korotkov.co.uk/f/1/d/1/1d137a02e6b2c874493efffb91d7377682.png)
. Тогда действительно из сравнения

следует сравнение
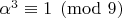
. Для доказательства достаточно записать

и заметить, что оба сомножителя делятся на

(нужно, конечно, ещё объяснить, почему).
P.S. На самом деле сравнение
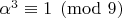
вытекает из сравнения

при любом
![$\alpha \in \mathbb{Z}[\omega]$ $\alpha \in \mathbb{Z}[\omega]$](https://dxdy-02.korotkov.co.uk/f/d/1/7/d1733f6f51ef124b4170395db14ad44d82.png)
.