Для функции

, заданной таблицей значений, найти ее приближенное значение в точке

, используя интерполяционные многочлены в форме Ньютона 1-й и 2-й степени. Оценить погрешность приближения по формуле остаточного члена.
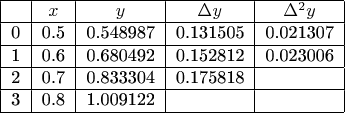


Я правильно формулы составил?
Как оценить погрешность приближения по формуле остаточного члена?