Хотя нет. Я представил
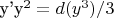
b и произвел замену

.
После получается уравнение

.
Решаю методом вариации произвольной постоянной и получаю
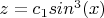
Вопрос: мне этот z подставить в ихсодное уравнение,предварительно записав

?
В вольфраме ответ

не понимаю откуда берется во втором аргументе 3 степень у икса