Решение нелинейных уравнений (Вычислительная математика)

[Sverest]

Для того чтоб найти решение нелинейного уравнения на отрезке с определенной точностью, надо поделить отрезок пополам, выбрать из получившихся отрезков тот на котором функция меняет знак, и так делать то тех пор пока длина отрезка не станет меньше заданной точности, а потом надо взять значение середины отрезка в качестве решения?

[svv]

Да, это Вы описали метод дихотомии (он же метод бисекций, он же метод половинного деления). Конечно, есть много других методов. Они описаны в любом справочнике по высшей математике.

[Sverest]

где посмотреть про метод итерации, попонятней, применительно к нелинейным уравнениям не подскажете?

-- Пт ноя 18, 2011 16:35:06 --

В википедии нашел:

Условие $f(x)=0\!$ преобразуется к виду $ x=\varphi(x)\!$ , где $\varphi(x)\!$ — сжимающая
Задаётся начальное приближение и точность $x_0, \quad \varepsilon, \quad i=0\!$
Вычисляется очередная итерация $x_{i+1}=\varphi(x_i)\!$
Если $||x_{i+1}-x_i||>\varepsilon\!$ , то $ i=i+1\!$ и возврат к шагу 3.
Иначе $x=x_{i+1}\!$ и остановка.

То есть если у меня функция $\ln x =4-x^2$ я ее должен привести к виду $x=\sqrt{\ln x -4}$

-- Пт ноя 18, 2011 16:36:11 --

а что значит:
Вычисляется очередная итерация $x_{i+1}=\varphi(x_i)\!$ ?

[svv]

Начинаем с какого-то $x_1$, подставляем в правую часть, вычисляем правую часть. То, что получилось, называется $x_2$.
Полученное $x_2$ подставляем в правую часть, вычисляем правую часть. То, что получилось, называется $x_3$.
И так далее. Каждый такой шаг называется итерацией.

[Sverest]

Что значит для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций

[ewert]

Какой-то оффтопик. Принцип сжимающих отображений не имеет ни малейшего отношения к методу половинного деления (или, что эквивалентно, дихотомии, или как уж ни называй).

[Sverest]

ewert в сообщении #505203 писал(а):

Какой-то оффтопик. Принцип сжимающих отображений не имеет ни малейшего отношения к методу половинного деления (или, что эквивалентно, дихотомии, или как уж ни называй).

У меня задание решить двумя способами

[svv]

ewert, вопрос был не о дихотомии, а о методе $x=f(x)$. А он-таки отношение имеет.

[ewert]

svv в сообщении #505208 писал(а):

ewert, вопрос был не о дихотомии,

Нет, я всё-таки хоть и немного умею, но всё-таки немного умею читать стартовые посты:

Sverest в сообщении #505095 писал(а):

надо поделить отрезок пополам,

-- Пт ноя 18, 2011 19:28:52 --

Sverest в сообщении #505204 писал(а):

У меня задание решить двумя способами

Тогда предъявите конкретное задание, Иначе разговор беспредметен.

[svv]

Ну, а потом (начиная с третьего сообщения в этой теме) речь зашла о другом методе.

[ewert]

(Оффтоп)

svv в сообщении #505213 писал(а):

Ну, а потом (начиная с третьего сообщения в этой теме) речь зашла о другом методе.

Ну а зачем, собственно?... вообще, прежде заводить хоть какой разговор -- почему бы не обозначить хоть предмет разговора, хоть краешком?...

Пока что же ветка вызывает впечатление не более чем троллинга. Возможно, и нечаянного; всяко случается.

[Sverest]

ewert в сообщении #505211 писал(а):

Тогда предъявите конкретное задание, Иначе разговор беспредметен.

Методом бисекции найти решение нелинейного уравнения $\ln x =4 -x^2$ на отрезке $[1,5; 2]$ с точностью $\varepsilon=10^{-2}$. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью $\varepsilon=10^{-4}$.
Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.

-- Пт ноя 18, 2011 19:02:38 --

Методом бисекции я получил значение $x_0=1,83984375$

-- Пт ноя 18, 2011 19:06:40 --

Методом итераций $1,84110108208045$ на третьей итерации

[Sverest]

Я оказывается неправильно решил:

Цитата:

Результаты надо оформить в виде таблицы, ее заголовок
$a$ ; $b $ ; $f(a) $; $f(b)$ ; $\frac{a+b}{2} $ ; $f(\frac{a+b}{2} )$

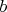
Надо сделать столько шагов, что бы точность была 0,01

При такой точности, найденные 8 цифр после запятой не имеют никакого смысла, они не являются верными.

В методе итераций не обоснована сходимость метода (достаточное условие)

В ответе указано лишнее количество цифр после запятой, что не соответствует заданной точности.

Посмотрите, правильно ли я сделал таблицу:
$\begin{tabular}{ccccccc} $a$ & $b$ & $f(a)$ & $f(b)$ & $\frac{a+b}{2}$ & $f(\frac{a+b}{2})$ & $b-a$ \\ \hline 1.5&2 &-1.34 & 0.69&1.750 &-0.378 &0.5 \\ 1,75& 2 &-0,38 &0,69& 1,875& 0,144& 0,25\\ 1,75& 1,875 &-0,38 &0,14& 1,813 &-0,120 &0,125\\ 1,813& 1,875& -0,12 &0,14 &1,844 &0,012 &0,062\\ 1,813& 1,844 &-0,12 &0,01& 1,829& -0,053& 0,031\\ 1,829 &1,844 &-0,05& 0,01& 1,837& -0,019& 0,015\\ 1,837 &1,844 &-0,02& 0,01& 1,841& -0,003& 0,007\\ \end{tabular}$

$x_0=1.841$