Здравствуйте! Помогите доказать, что если бесконечное пространство

, является непрерывным образом пространства

при замкнутом отображении, то существует такое кардинальное число
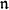
, что

.

- пространство, состоящее из множества

мощности

и семейства открытых подмножеств, каждое из которых либо не содержит некоторую точку

либо имеет конечное дополнение.
Я понимаю, что топология на

порождается семейством замкнутых множеств

, но это не значит, что если

- конечно и не содержет

, то оно замкнуто в

. Дальше ступор.
Благодарю.