Сходимость знакопеременного ряда (проверка на WolframAlpha)

[astrophonic]

Добрый вечер!
Мне необходимо исследовать на сходимость ряд:
$ a_{n} = \sum^{\infty}_{n=1} {\frac{(-1)^n (n+3)}{\ln(n+4)}}$
$u_{n} = \lvert a_{n} \rvert = \sum^{\infty}_{n=1} {\frac{(n+3)}{\ln(n+4)}} $
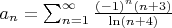
Считаю:
$\lim_{n \rightarrow \infty} \frac{n+3}{\ln(n+4)} = \infty$
получается, что ряд, составленный из модулей его членов, расходится.
Теперь стоит вопрос:$ a_{n}$ расходится или условно сходится?
По Лейбницу он должен либо монотонно убывать(а он не убывает),либо $\lim_{n \rightarrow \infty} \frac{n+3}{\ln(n+4)} = 0$, что я уже посчитала и выходит бесконечность. Получается, что он расходится.
Решила проверить себя на WolframAlpha и вышло, что:
$ a_{n} = \sum^{\infty}_{n=1} {\frac{(-1)^n (n+3)}{\ln(n+4)}} \approx -1.16464$
Подскажите, в чем ошибка.

[ИСН]

Если путать ряд и член ряда, то совершенно естественно допустить также пару опечаток при вводе на Альфу, а уж тогда - - -

-- Чт, 2011-09-22, 23:02 --

Выводы головой, впрочем, верные.

[LaTeXScience]

astrophonic в сообщении #485336 писал(а):

Решила проверить себя на WolframAlpha и вышло, что:
$ a_{n} = \sum^{\infty}_{n=1} {\frac{(-1)^n (n+3)}{\ln(n+4)}} \approx -1.16464$
Подскажите, в чем ошибка.

Sum does not converge.

[astrophonic]

ИСН в сообщении #485338 писал(а):

Если путать ряд и член ряда

Вы про эту запись, да?$$ a_{n} = \sum^{\infty}_{n=1} ...
LaTeXScience, утром на свежую голову поняла в чем у меня проблема на вольфраме. Он выводит мне Approximated sum. Вчера не заметила. И даже на график частичных сумм не взглянула.

Всем спасибо!