Направьте пожалуйста - как гладкость ( то есть существование непрерывной производной для всей кривой) соотносится с корнями кубического полинома?

. Если корень многочлена под радикалом простой, то при кривая пересекает горизонтальную ось в этой точке вертикально и, соответственно, кривая (именно
кривая, а не функция

) оказывается гладкой. Если корень двукратный, то кривая подходит к оси и снизу, и сверху под ненулевым углом, т.е. в этой точке получается излом. Если же корень трёхкратный (что, впрочем, возможно лишь при
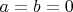
), то получится вообще клювик.
да, спасибо, я вообще это для задач криптографии рассматриваю, а там мы рассматриваем эллиптическую кривую над некоторым абстрактным полем, и само понятие производной чисто формально, однако нам как раз и нужно, чтобы не было "клювиков" и самопересечения, это кстати легко представить если посмотреть на кривую в


при наличии кратных корней мы например имеем

и кривая будет иметь как раз самопересечение, что не удовлятворяет требованию гладкости
верно?