
Доказать исходя из определения, что последовательность неограничена.
Неограниченная последовательность - это последовательность, которая не является ограниченной.

неограниченная

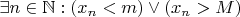
Любая неограниченная последовательность расходится.
Если предел

существует и

конечно, то говорят, что числовая последовательность сходится. В противном случае последовательность расходится.
То есть нужно доказать, что последовательность расходится, то есть не имеет предела?