Вы каким-то общим методом решаете?
После замены

получаем:
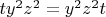
. Отсюда сразу видно мое решение.
Но это еще не все. В книгах (напр., Магнус, Каррас, Солитер "Комбинаторная теория групп", Линдон, Шупп "Комбинаторная теория групп") Вы можете найти общее решение уравнения

в свободной группе и из него, повидимому, получить еще решения Вашего уравнения (но с этим нужно повозиться).