Пересчитайте после добавления ещё одной карточки с двумя буквами В.
Если у нас всего одна карточка с буквами А на обоих сторонах, и всего одна карточка с буквами А и В,
и если при этом выпала карточка с буквой А, то нас не интересует, сколько там карточек с буквами В на обоих сторонах.
Если же мы добавили, скажем, ещё одну карточку с буквами В на обоих сторонах, и выпала карточка с буквой В на лицевой стороне, то, естественно, вероятность того, что на обороте окажется тоже буква В, увеличится с

до
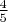
.