1) Выберем любых 2 из

, которые не сражались между собой. По условию каждый из них сразился минимум с

других боксёров, а так как без наших двух всего
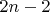
боксёров, то есть хотя бы 2 других боксёра, с которыми они оба сражались. Эта четвёрка и будет искомой.