Решение
Уравнение

образуется следующим образом[

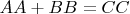





Уравнение

имеет решение для всех целых чисел.
Уравнение

имеет решение не для всех целых чисел. Исключительно для троек Пифагора.
Тройки Пифагора имеют свойство.
Для каждой Тройки, для каждого С имеется только одно сочетание целых А и В.
Берем тройку 3 4 5

не 125.
Не трудно убедится , что так будет для всех пифагоровых троек.
Если доказано, что в уравнении


всегда не целое, то и

число всегда не целое.
Далее, по аналогии, для всех N.