Все подмножества непустого конечного множества

изначально были чёрными.
Затем некоторые из них покрасили в белый цвет так, что для любых двух белых подмножеств

и

(не обязательно различных)

- тоже белое.
а) Доказать, что для любых двух белых подмножеств

и

(не обязательно различных)
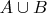
- тоже белое.
б) Какого цвета может быть пустое подмножество? А само множество

?
в) Что можно сказать о чётности числа белых подмножеств? Каково минимальное число белых подмножеств, если есть хотя бы одно белое подмножество? А если есть хотя бы одно белое непустое собственное подмножество?
а) Возьмём два белых подмножества

и

, для них подмножество

- белое. Тогда для двух подмножеств

и

подмножество

тоже белое
б) если

-белое, то

- тоже белое, тогда

- тоже белое. Ну и

- тоже белое.
в) Для каждого белого подмножества

подмножество

- тоже белое. Поэтому число белых подмножеств чётно.
минимально 2 белых подмножества:

и

.
ну и на последний вопрс: 4 белых подмножества.

,

,

и
