Короче, вот кусочек из моего конспекта, хотя советую открыть нормальный учебник и прочитать там.

,

— неизвестны;

,

,

,

— распределена по Стьюденту с

степенью свободы, не зависит от

; находим

, где
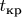
— двустронняя критическая точка, соответсвующая

,

, с вероятностью

имеем

,

,

; т.о.,
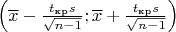
— доверительный интервал для

с коэффициентом доверия

.