Тогда такой вариант.

— множество термов. Строим функцию

,

— множество индексов документов, которые содержат

.

, каждый элемент

заменяем на какой-нибудь элемент

и получаем

, которое есть идентификатор документа с индексом

. Далее можно попытаться уменьшить

, просто перебирая подмножества и проверяя их на корректность.
Критерий, который задаёт корректное решение для документа с некоторым индексом
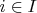
, не зависит от решений для других документов, поэтому оптимальное решение для каждого
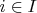
ищется независимо.