Nogin Anton, сложно понять, что у вас происходит в формулах. Попробуйте что-нибудь врое:
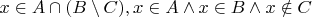
Код:
x \in A \cap (B \setminus C), x \in A \wedge x \in B \wedge x \notin C
maxmatemТопикстартер так и пытается, но что-то у него не заладилось... увы, не могу понять, что именно.
Ну хорошо, смотрите, слева у вас есть

, а справа —
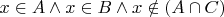
. Правая часть мясистее, поэтому ее надо обкромсать до левой части, главное, аккуратно раскройте непринадлежность пересечению. А если вы пойдете слева направо, то в жизни не догадаетесь, что там надо пририсовать.