С помощью множителей Лагранжа решить задачу

[Иван_85]

С помощью множителей Лагранжа решить задачу:
$-4x-2y\to \min$, $4x+2y-8=0$, $16x^2+4y^2-64\le 0$.
Для начала я решаю задачу только с уравнением-связи.
Функция Лагранжа:
$L(x, y, \lambda)=-4x-2y+\lambda (4x+2y-8)$;
$\frac{\partial L}{\partial x}=-4+4\lambda=0$,
$\frac{\partial L}{\partial y}=-2+2\lambda=0$,
$\frac{\partial L}{\partial \lambda}=4x+2y-8=0$.
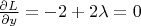
Получаем $y=4-2x$, то есть целевая функция принимает минимум на всей прямой $y=4-2x$.
Теперь к изначальной задаче.
$16x^2+4y^2-64\le 0$,
$\frac{x^2}{2^2}+\frac{y^2}{4^2}\le 1$ - область эллипса с границей.
В итоге получаем, что целевая функция принимает минимум на отрезке прямой
$y=4-2x$, $0\le x \le 2$.
Я правильно решил?
Интересует еще такой вопрос, можно ли неравенство-связь как-нибудь запихнуть в функцию Лагранжа?

[мат-ламер]

Иван_85 в сообщении #431202 писал(а):

Я правильно решил?
Интересует еще такой вопрос, можно ли неравенство-связь как-нибудь запихнуть в функцию Лагранжа?

1) Правильно.
2) Можно. А что дальше делать будете?

[Иван_85]

Дальше ничего делать не надо.
А где можно посмотреть про то как можно засунуть неравенство-связь в функцию Лагранжа? Смотрел в Зориче, там ни слова.

[Алексей К.]

Как-то я не заметил, что решалась задача именно на минимум.
Ведь на максимум она решалась бы так же.
А проверяя, минимум это или максимум, мы легко обнаружим, что это константа, такой же минимум, как и максимум.
Я не уверен, что об этом следует умалчивать в решении.

[мат-ламер]

Иван_85 в сообщении #431216 писал(а):

А где можно посмотреть про то как можно засунуть неравенство-связь в функцию Лагранжа? Смотрел в Зориче, там ни слова.

Если рассматривать задачи с ограничениями-неравенствами, то оптимальная точка является седловой для функции Лагранжа (при вып. некоторых условий). В любом учебнике по методам оптимизации можно посмотреть. См. параграфы про теорему Куна-Таккера.

[bot]

А зачем вообще здесь множители Лагранжа? Внутри окружности ни наименьшего ни наибольшего значения очевидно быть не может, следовательно они на окружности. Так как есть ещё одно уравнение связи - прямая, то проверке подлежат всего две точки. В одной из них наибольшее, в другой наименьшее значения.

[ewert]

Иван_85 в сообщении #431216 писал(а):

А где можно посмотреть про то как можно засунуть неравенство-связь в функцию Лагранжа?

Боюсь, что нигде и никак.

Кроме того, у Вас условие наверняка было не таким: заставлять искать минимум/максимум линейной функции на прямолинейном отрезке, да ещё и Лагранжем -- нелепо. Наверняка имелись в виду максимум/минимум в области, заданной двумя неравенствами, т.е. в кусочке эллипса, отсечённым прямой (которая, кстати, проходит через две соседние вершины эллипса).

[Null]

Мы проходили как неравенства в уравнения Лагранжа включать.
В Алексееве, Галееве, Тихомирове "Сборник задач по оптимизации" есть.