Интеграл, содержащий Бесселевы функции

[chpv]

При решении задачи возникла необходимсоть вычислить определённый интеграл вида:
$\int\limits_{0}^{1}\ rJ_{0}(ar)J_{1}(br)\, dr$

Наиболее фундаментальная информация по Бесселевым функциям содержится в книге Ватсона Г. Н. "Теория Бесселевых функций" не дала ответ мне на поставленный вопрос.

В ней содержится исследование интегралов похожего вида (Ватсон Г. Н. "Теория Бесселевых функций" параграф 13.44), например
$\int\limits_{0}^{\infty}\ t^{-\lambda}J_{\mu}(at)J_{\nu}(bt)\, dt$

Однако превиденное Вассоном исследование интеграла не дает возможность применить его к вычислению требуемого.
Стоит заметить, что определённые интегралы исследуемые в книге Ватсона имеют верхний предел интегрирования равный бесконечности ($\infty$), а интеграл который необходимо мне вычислить имеет верхний предел интегрирования равный единице ($1$).

Буду очень признателен, если подскажете метод и возможные пути решения поставленной задачи.

[nestoklon]

Есть такая замечательная книжка: Градштейн И.С. Рыжик И.М. "Таблицы интегралов, сумм, рядов и произведений". Если там нет, значит не берётся.
Я глянул -- там есть очень похожий интеграл номер 6.521. А такого не нашёл. Но поищите лучше сами.

[chpv]

nestoklon в сообщении #429805 писал(а):

Есть такая замечательная книжка:...

Спасибо большое за информацию, сейчас посмотрю его.

Однако хотелось бы узнать как вообще подобные интегралы искать.
Какими методами и какими подходами.
Вот например как Грандштейн с соратниками подобные интегралы находили?

-- Пт апр 01, 2011 09:22:24 --

nestoklon в сообщении #429805 писал(а):

есть очень похожий интеграл номер 6.521. А такого не нашёл...

Интеграл действительно похожий, но вот функции бесселя там одного порядка $\nu$, а в интеграле который следует вычислить первая функция бесселя нулевого порядка, а вторая функция бесселя - первого порядка.

Проблема остается открытой.

[profrotter]

Что если попробовать интегрирование по частям, а потом учесть, что $\frac {dJ_0(x)} {dx}=-J_1(x)$ и $\frac {dJ_1(x)} {dx}=J_0(x)-\frac {J_1(x)} x$?

[nestoklon]

chpv в сообщении #429809 писал(а):

Вот например как Грандштейн с соратниками подобные интегралы находили?

Там есть ссылка. В конце книжки есть список литературы. Но обычно или желаемый интеграл просто получается из того что можно найти в этой книжке (например так как предлагает profrotter) или он не берётся.

[Vince Diesel]

Математика дает
$\int\limits_{0}^{1}\ rJ_{0}(ar)J_{1}(ar)\, dr= \frac{1}{6} a \, _2F_3\left(\frac{3}{2},\frac{3}{2};2,2,\frac{5}{2};-a^2\right)$
Для разных $a$ и $b$ не считает. Так что, может, и ответа хорошего нет.

[chpv]

profrotter в сообщении #429822 писал(а):

Что если попробовать интегрирование по частям...

Уважаемый profrotter, спасибо за совет, попробую это проделать. О результатах сообщую.

-- Пт апр 01, 2011 12:04:15 --

Vince Diesel в сообщении #429827 писал(а):

Математика дает
$\int\limits_{0}^{1}\ rJ_{0}(ar)J_{1}(ar)\, dr= \frac{1}{6} a \, _2F_3\left(\frac{3}{2},\frac{3}{2};2,2,\frac{5}{2};-a^2\right)$
Для разных $a$ и $b$ не считает. Так что, может, и ответа хорошего нет.

Vince Diesel, спасибо. Я пробовал численно посчитать в Mathcad, при это задавал требуемый интеграл и задавал разные $a$ и $b$. Программа выдала числовой результат и не выругалась, значит в ней есть механизмы расчета.

Пробовал решать интеграл в MATLAB с разными $a$ и $b$, результат был неудовлетворительный, так как MATLAB не может это делать для разных $a$ и $b$.

[Vince Diesel]

Числовой, это с десятичной точкой что ли? Если так, то это не показатель.

[ewert]

chpv в сообщении #429836 писал(а):

MATLAB не может это делать для разных $a$ и $b$.

Что значит "не может"? Запрограммируйте сами подынтегральную функцию со ссылкой на встроенные функции Бесселя. И определите внутри этой функции параметры как глобальные.

[chpv]

ewert в сообщении #429847 писал(а):

Что значит "не может"? Запрограммируйте сами подынтегральную функцию со ссылкой на встроенные функции Бесселя. И определите внутри этой функции параметры как глобальные.

Спасибо за совет, попробую, но пока не совсем прозрачно для меня это выглядит. В любом случае MATLAB считает интегралы через символьную бибилотеку (syms). И получится ли его "обмануть" таким образом не знаю, пока не пропробую.

-- Пт апр 01, 2011 13:46:06 --

Vince Diesel в сообщении #429842 писал(а):

Числовой, это с десятичной точкой что ли? Если так, то это не показатель.

Да, с десятичной точкой в виде $...=0.643$.
И почему не показатель? Хотитет сказать что он что-то считает и не понятно что считает, т.е. результат его вычислений не является результатом вычисления определённого интеграла с заданными числами $a$ и $b$?

[Vince Diesel]

Так то численные методы интегрирования, сейчас пакеты от чего что угодно достаточно гладкого интеграл посчитают, а надо замкнутая форма, наколько я понял.

[svv]

Янке, Эмде, Лёш. Специальные функции. Формулы, графики, таблицы.
Страница 245, пункт "Формулы интегрирования".

Там есть очень похожие неопределенные интегралы (например, $\int r J_0(ar) J_0(br) dr$), в том числе даже более сложные, чем Ваш. Но Вашего, к сожалению, там нет. Вывод: находите численно.

[chpv]

svv
Спасибо, я Янке смотрел уже, да похожие есть, но все же это не то что необходимо вычислить.

Vince Diesel
Был бы очень признателе если бы получил от Вас вводный курс о том чем плох метод вычисления интеграла которым пользуются математические пакеты и чем конечный результат вычисления математического пакета отличается от вычисления замкнутой формы. Кстати, что Вы понимаете под "замкнутая форма"?

Возможно решение поставленной пробелмы будет другое, если я приведу изначалый интеграл, после преобразование которого получен интерграл в первом посте.
Изначально проблемы выглядела следующим образом:
$\int\limits_{0}^{1}\ rJ_{0}(ar)\frac{dJ_{0}(br)}{dr}\, dr$
После вычислений получаем:
$-b\int\limits_{0}^{1}\ rJ_{0}(ar)\ J_{1}(br)\, dr$
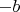
который и равен, за исключением постояного множителя перед интегралом ($-b$), интегралу в первом посте.

Попробую вычислить его, как мне уже тут советовали, интегрированием по частям с соответсвующими заменами.

[vark]

Могу порекомендовать "Специальные функции и теория представлений групп", Виленкин Н.Я.

[chpv]

Спасибо vark большое, обращусь к этой литературе обязательно.