Дело,наверное,в том,что первая система уравнений имеет и положительные и отрицательные решения (ясно,что

и

имеют одинаковые знаки,кроме того,если одновременно поменять знаки

и

,то уравнения системы не изменятся) ,поэтому имеет смысл находить

.В то же время,даже не решая последнюю систему,можно сказать,что для нее

неотрицательны (из-за неравенства
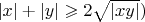
и для нее

не имеет смысла.