Цитата начала параграфа 8 первой главы из книги "Основы теоретической логики" Гильберта, Аккермана:
Цитата:
§ 8. Дополнительные замечания к проблеме всегда-истиннсти (*) и выполнимости.Установленную в предыдущем параграфе совершенную нормальную форму
(*) для выражения, которое состоит из основных высказываний
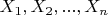
, мы будем также называть кратко
разложением выражения по 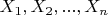
.
Пусть теперь нам дано некоторое сложное высказывание, в котором содержаться, кроме
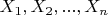
, ещё основные высказывания

.
И в этом случае мы можем говорить в известном смысле о разложении по 
. А именно, можно представить выражение в виде
конъюнкции, у которой каждый конъюнктивный член является дизъюнкцией выражения, зависящего только от  , и одной из конституент (**) от
, и одной из конституент (**) от 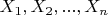 .
.
Доказательство очень простое. Достаточно лишь разложить выражение по всем имеющимся основным высказываниям, т.е. по  , и соединить вместе члены, содержащие одинаковые по отношению к
, и соединить вместе члены, содержащие одинаковые по отношению к 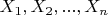 конституенты.
конституенты. * - под
всегда-истинностью высказывания подразумевается
тавтология** - тут имеется ввиду
совершенная конъюнктивная нормальная форма*** - конституент в данном случае означает
конъюнктивный член совершенной конъюнктивной нормальной формыВопросы:1)
Что вообще автор хотел этим сказать?2) Что
тут значит фраза "в известном смысле" в предложении
И в этом случае мы можем говорить в известном смысле о разложении по 
?
3) В предложении:
А именно, можно представить выражение в виде конъюнкции, у которой каждый конъюнктивный член является дизъюнкцией выражения,
зависящего только от  , и одной из конституент от
, и одной из конституент от 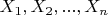 .
.Значит ли это, что:
выражение можно представить в виде несовершенной конъюнктивной нормальной формы, где каждый конъюнктивный член содержит дизъюнкцию всех

(где, могут быть повторения любого

, так как вся форма несовершенна, но они должны быть обязательно все) и в этом же конъюнктивном члене к нему прикреплен конституент (то есть член от совершенной формы) от
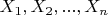
Или же это значит, что:
в этой несовершенной нормальной форме, каждый конъюнктивный член построен так, что
вне зависимости от значений основных высказываний
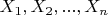
, результат таблицы истинности определяет только та часть члена, в которой фигурирует
 ?
?4) Что
тут значит фраза
содержащие одинаковые по отношению?
5) Или как называется
именно эта теорема и где её можно найти? Обычно когда мне что-то непонятно, то я смотрю
это же у другого автора, но именно это утверждение я не нашел.