Вот это, как мне кажется, надо рассказывать студентам даже в стандартном курсе анализа.
(Обсуждение того, является ли стандартным курс анализа, в котором нет понятий метрическое пространство, полнота, гомеоморфизм метрических пространств, я сразу оставляю профессиональным педагогам, мне это не интересно)
Рассмотрим метрическое пространство

с метрикой

и метрическое пространство
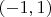
с той же метрикой. Эти пространства гомеоморфны, однако, одно из них полно, а другое нет.
Тоже, но вид сбоку. В пространстве

метрики

и

задают одну и туже топологию. Но последовательность

в смысле одной метрики является последовательностью Коши, а в смысле другой- нет.