Отображения

[Xoma]

Помогите пожалуйста понять решение примера
Выяснить во что преобразуется при отображении $w=ch(z)$
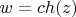
Полоса G:$0<Imz<\pi$
После преобразований у них получается что при
1)$y=0 ,u=ch(z),v=0$
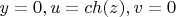
2)$y=\pi, u=-chx, v=0$
Тут все понятно а дальше они пишут:
Функция w=ch(z) отображает полосу G на всю плоскость с разрезами по лучам
$(-\infty;-1],[1;+\infty)$
Почему у них именно так получилось?объясните пожалуйста
Завтра сдавать уже

[paha]

Xoma в сообщении #391209 писал(а):

Функция w=ch(z) отображает полосу G на всю плоскость с разрезами по лучам
$(-\infty;-1],[1;+\infty)$

$\ch x\ge 1$

[Xoma]

т.е там на отрезке [-1;1] будет как бы белая не закрытая полоса?
Что значит с разрезами по лучам $(-\infty;-1],[1;+\infty)$?
это когда по оси u выкалываются точки $(-\infty;-1],[1;+\infty)$?

[paha]

Xoma в сообщении #391212 писал(а):

т.е там на отрезке [-1;1] будет как бы белая не закрытая полоса?

этого не понял

Xoma в сообщении #391212 писал(а):

Что значит с разрезами по лучам $(-\infty;-1],[1;+\infty)$?

значит плоскость без этих лучей

[Xoma]

А почему здесь будет без этих лучей? это по оси u?

-- Сб дек 25, 2010 03:31:42 --

"этого не понял "
Ну там ведь u будет больше или равно 1 и меньше -1
поэтому область будет без полосы от -1 до 1 ?разве не так?

[paha]

Xoma в сообщении #391222 писал(а):

Ну там ведь u будет больше или равно 1 и меньше -1
поэтому область будет без полосы от -1 до 1 ?разве не так?

не так... этих разрезов нет потому, что это образы прямых, ограничивающих полосу ($\ch x\ge 1$ для $x\in\mathbb{R}$), а все остальное -- в образе отображения... например $\ch{i\pi/2}=0$

[antbez]

У меня вопрос по общей теории отображений. Известно, что при определении этого понятия предполагается, что элементу x соответствует при отображении единственный элемент y. А вот если эта единственность нарушается? Есть ли термин для подобного отображения? Что-нибудь вроде "дезъекции"?

[Joker_vD]

antbez
"Многозначная функция" вас устроит?

[antbez]

Joker_vD в сообщении #400167 писал(а):

antbez
"Многозначная функция" вас устроит?

Нет. Это и так понятно, что она- многозначна. Хотелось бы специального термина!

Может быть, согласимся на "полиекции"?

[Joker_vD]

antbez в сообщении #400391 писал(а):

Хотелось бы специального термина!

Так это и есть специальный термин. Если не нравится, называйте "отношением".

[paha]

antbez в сообщении #400103 писал(а):

А вот если эта единственность нарушается?

Тогда у Вас отображение не в $X$, а в множество подмножеств из $X$, только и всего... область значений меняется

[antbez]

Только у меня отображение в Y. Я понимаю, как "сузить" моё отображение (изменяя область значений) до выполнения единственности, я спрашивал лишь о термине.