Здравствуйте! Помогите доказать тождество:
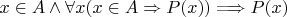
.
Вот если бы здесь не было квантора

, то было бы легко:
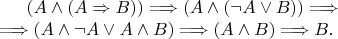
А вот, что делать с квантором? Спасибо!
Что делать с квантором я не знаю.
Помогите доказать тождество:
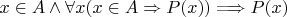
.
А теперь попробуем доказать, что это высказывательная форма истинна при всех значениях переменной

. Во-первых мы должны предположить, что высказывательная форма определена на некотором множестве

. Во вторых, что
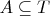
. Поскольку ничего специфического про

не сказано, то могут существовать такие

, что

истинно, но могут существовать и такие

, что

ложно. При этих допущениях воспользуемся формулой

. Получаем:
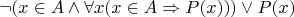
.
Преобразуем эту форму так:
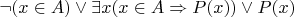
. Получили дизъюнкцию. Разберите случаи.