Стационарное или нестационарное УШ - это выбор между
![$$i\frac{\partial}{\partial t}\Psi=H\Psi=\left[-\frac{1}{2m}\frac{\partial^2}{\partial x^2}+U(x,t)\right]\Psi\eqno(\text{НстУШ})$$ $$i\frac{\partial}{\partial t}\Psi=H\Psi=\left[-\frac{1}{2m}\frac{\partial^2}{\partial x^2}+U(x,t)\right]\Psi\eqno(\text{НстУШ})$$](https://dxdy-02.korotkov.co.uk/f/d/e/e/dee2cfd90d578f96d01b47733a68f5b182.png)
и
![$$E\psi=H\psi=\left[-\frac{1}{2m}\frac{\partial^2}{\partial x^2}+U(x)\right]\psi,\eqno(\text{СтУШ})$$ $$E\psi=H\psi=\left[-\frac{1}{2m}\frac{\partial^2}{\partial x^2}+U(x)\right]\psi,\eqno(\text{СтУШ})$$](https://dxdy-03.korotkov.co.uk/f/6/d/1/6d17c887c8a19e763042b3ce87e2fc8a82.png)
причём (НстУШ) называется
нестационарным, даже когда

не зависит от

Переход от (НстУШ) к (СтУШ) отвечает стационарности
решений, то есть на физическом языке - стационарности состояний квантовой системы. Решение (НстУШ) называется стационарным (физически - стационарным состоянием), когда раскладывается на множители

(разумеется, для этого должно быть

) а решения такого вида можно найти, разделив в (НстУШ) переменные, и получив по одной из переменных (СтУШ), а по другой - тривиальное

В области

оба уравнения имеют решения в виде суперпозиции плоских волн, но для (НстУШ) в суперпозиции участвуют волны вида

для всех

и для
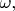
удовлетворяющих дисперсионному соотношению

а для (СтУШ) участвуют только волны вида

где

выбираются из дисперсионного соотношения

но при фиксированном для всего уравнения в целом

Таким образом, задача рассеяния в стационарной формулировке рассматривает в области падения волну вида

а в нестационарной формулировке уже

где

а

(Разумеется, если бы речь шла о более общем рассеянии на времязависимом потенциале, а не о бусте стационарного потенциала, отражались бы волны всевозможных энергий, и требовалось бы нечто вида

) Теперь видно, какие функции и как должны сшиваться, а в какой точке - зависит от потенциала

Если мы берём неподвижную ступеньку, до буста, то сшивка происходит в точке

Только тогда,
после решения условий сшивки, можно будет констатировать, что отражённая волна имеет тот же временной множитель

и поэтому его можно вынести за скобку, и перейти от (НстУШ) к (СтУШ). А если мы берём движущуюся ступеньку, то сшивка происходит в точке

и разумеется, будет

и решение условий сшивки... вот теперь можете найти его сами.