количество вершин не надо "задавать")
Надо строить триангуляцию интересующего пространства и подсчитывать -- сколько вершин получилось
У каждого 2-симплекса три ребра, но поверхность без края -- поэтому любое ребро триангуляции принадлежит ровно двум различным симплексам (мы неявно подразумеваем триангуляцию "хорошей" -- нет 2-симплексов, склеивающихся сами с собой, хотя и это не запрещено), отсюда и
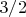
.
Если Вы построили триангуляцию тора с

2-симплексами, то количество вершин, очевидно, будет

, а у проективной плоскости

.
-- Пт окт 29, 2010 22:03:53 --Вот еще забавная схема. Пусть поверхность склеена из равносторонних треугольников так, что каждый треугольник инцидентен трем ребрам и трем вершинам триангуляции (граница треугольника -- петля без самопересечений на на поверхности).
Допустим, имеется

вершин,

ребер и

треугольников. Пусть также в

-ой вершине сходятся

треугольников. Ясно, что

.
Полный угол около каждой точки на такой поверхности равен

за исключением вершин. В

-ой вершине полный угол равен

(ведь там сходятся

треугольников, причем каждый -- с углом

).
Кривизна в

-ой вершине равна

.

мы доказали теорему Гаусса-Бонне для замкнутых поверхностей.