Помогите, пожалуйста, разобраться с доказательством.
Даны два множества:

;

,
здесь

-
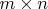
матрица.
Нужно доказать, что если

- экстремальная точка

, то

, где

- экстремальная точка

.
Рассуждения: предположим противное, т.е.

- экстремальная точка

,

, но здесь

не является экстремальной точкой

.
Это означает, что существуют точки

.
Умножив это равенство слева на матрицу А, получим

или

, что противоречит тому что

- экстремальная точка.
В этом доказательстве мне непонятно, как мы можем знать, что

. Кто-нибудь может помочь? Спасибо.